　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　風と翼 Windandwing は、c++の数値計算から風と翼の計算へを目的とした数値計算を行っています。

Addres http://www5.synapse.ne.jp/windandwing/

c++ 数値計算 7 数値積分(離散系 ) 不等間隔データの積分(Newton-Cotes法)

第9章数値積分(離散系) 　等間隔、不等間隔データ(Newton-Cotes法)、級数展開

等間隔の離散データの数値積分
　等間隔の離散データを用い数値積分を行う場合、例えば Legendre 多項式で級数展開を行う場合は、データ個数の問題を除けば、台形則、Simpson1/3 則、Simpson3/8 則、Boole 則を積分手法として適用できる。あるいは、各種の補間法を用い新たに生成したデータにより、Gauss-Legendre積分計算等々を適用し、積分出来るかも知れない。

　このような等間隔の離散データの例として、前章の数値積分(連続系)で行った手法、数値積分(台形則、Simpson1/3 則、Simpson3/8 則、Boole 則)を用い、Chebyshev 多項式 t11 に対して Legendre 多項式の級数展開の計算を行った。

この離散データの数値積分の計算は、不等間隔データの数値積分を行うための前段階の説明である。

不等間隔あるいは不均等間隔の離散データの数値積分
　不等間隔の離散データに対して、数値積分を行う場合は、2次式のSimpson1/3則、3次式のSimpson3/8 則、4次式の Boole 則等々を直接に適用する事は出来ないので、それぞれの式が簡易な扱いに整理される前の計算方式で計算しなければならない。

　簡易な扱いに整理される前の計算方法である、 2、3 次の積分式で計算を行った。これらの計算方法は Lagrange 補間の多項式から求める事が出来る。

　　　　　　

このページの先頭へ

等間隔の離散データの数値積分(Newton-Cotes法)

1、離散データへの Legendre 多項式の級数展開の適用 (コード 1 )
　　前章では、連続した関数に対して級数展開を行った。この節では、[-1,1] 区間の Chebyshev 多項式 t11 の
　離散データ( 120 等分)に　Newton-Cotes法(台形則、Simpson1/3 則、Simpson3/8 則、Boole 則)で、
　Legendre 多項式の級数展開を行った。

　　これらの直交関数は、類似した構造(三角関数で関連付けられる)のために、計算がスムーズに行くと予想され
　るので、両者を選択した。Legendre 多項式を Chevyshev の多項式で、展開するのは、なんとなくフーリエ展
　開するのと同じと感じたから。単に高調波の集団に分けているから。曲線の集団の方が非実用的で面白い。

　　なお、コード 1 の計算は、不等間隔の離散データの数値積分の級数展開(次次節)でも計算出来る。

　　それぞれの級数の係数をLegendre6分点での係数と比較する事により、これらの積分手法の精度比較を行
　った。結論として、 1分割に 4個のデータを必要とする 30 分割 (30・4 = 120個)の Boole 則が精度が高い。

　　この比較は、120 個のデータにより台形則で係数を求める方法、あるいは、120 個を60 個の離散データとし
　て Simpson1/3 則( 120 個のデータ使用)で求める方法、また、40 個のデータでの Simpson3/8 則( 120 個使
　用)、更には、30 個のデータでの Boole 則( 120 個使用)で求める方法で、いずれの方法が同じデータを用いて、
　より高い近似になるのかを知る事を目的とした。

2、離散データ (下表)
　　 x は、[-1,1] を 120 等分し、この x に対応した Chebyshev ｔ11 の離散データ( g(x) )を示す。

　　　　　　　　　　

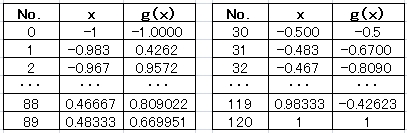
3、級数展開の係数
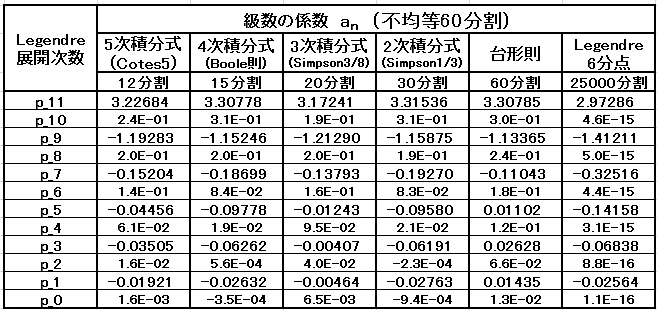
　　120 個のデータの台形則、60 個とした Simpson1/3則、40 個の Simpso3/8則、30個の Boole則の積分手
　法で得た Legendre 多項式の級数展開の各次数の係数を下表に示す。

　　同じ120個のデータを、30の区分分割数とした Boole 則が数値積分Legendre6分点の係数との比較で良い。
　この結果は、数値計算5 直交関数 Legendre多項式の直交性確認からでも推定できる。

　　　　　

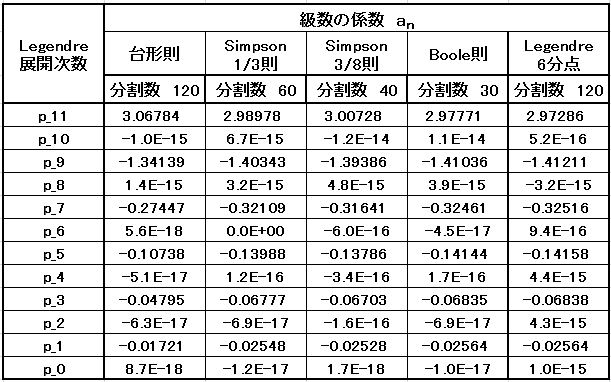
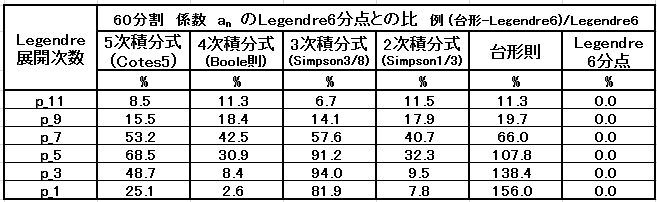
　　また、上記の各係数の値をLegendre6分点法の算出値との差比 % で示した表を下にしめす。Boole 則が精
　度が良いのは前記の通りである。3 次式近似に対応する Simpson 3/8 則が、2 次式近似に対応する
　Simpson 1/3 則より精度が悪い。これは、それぞれの持っている誤差によると考えられる。
　
　　Simpson 3/8 則より、Simpson 1/3 則が、数値計算でよく用いられるのは、この精度のよさによるのでは
　ないかと考える。

　　　　　

　　　　　　　　　　　　

このページの先頭へ

不等間隔の離散データの数値積分(Newton-Cotes法)

1.不等間隔の離散データの数値積分の方法 (コード 2)
　　不等間隔のデータに対して、2 次式の Simpson 1/3 則、3 次式の Simpson 3/8 則、4 次式の Boole 則を
　適用する場合は、それぞれの式が簡易な扱いに整理される前の計算で行う必要があり、これらは Lagrange 補
　間の多項式から求める事が出来る。

　1)不等間隔の離散データ用 2 次式( Simpson 1/3 則の原形) の算出
　　平面 (x , y) の 3 点を通る式は多数あるが、 2 次式に限定すれば、9-C-2式になる。
　　　　　
　　その 3 点を

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　9-C-1式　

　　とすると、Lagrange 補間多項式は、以下で示される。

　　　

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 9-C-2式

　　次に、9-C-2式が 3 点を通る 2 次式である事を示す。
　　この式に、x=x₀ を代入すれば、第 1 項の分子は分母と同じになり、y₀ の係数項が 1 となり、第 1 項は、
　　ｙ₀ となる。第 2 項と第 3 項は、(x-x₀) の部分が、(x₀-x₀) となるので、ゼロとなる。
　　従い、 y(x₀)=y₀ となる。

　　同様に、x₁、x₂ を代入すれば、y(x₁)=y₁、y(x₂)=y₂ となる。
　　これらにより、9-C-2式は、3 点を通る 2 次式である事になる。

　　上記の式を積分すると、以下の式 9-C-3 式となる。

　　　

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 9-C-3式

　　9-C-3式の第 1 項の積分を具体的に行う。

　　　
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　9-C-4式

　　9-C-4式で、定数項を除いた積分記号の個所を積分する。

　　　
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　9-C-5式

　　上式 9-C-5 式は、(x₂-x₀) を因子に持つので、下式となる。

　　　　
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　9-C-6式

　　　なお、上式を整理した下式で、2x₀² - x₂x₀ - x₂² を凝視すると、2a² - ab - b² = (2a + b)(a - b)
　　が浮かぶ。

　　　　
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 9-C-7式

　　従い、第 1 項の積分は、以下となる。下式で、分母の x₀ 、x₁ の括弧内の互いの位置に注意。

　　　
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 9-C-8式

　　　　　　　　　　　　　　　　　　
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 9-C-9式

　　次に、9-C-2 式の第 2 項を計算する。

　　　
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 9-C-10式

　　積分個所を積分すると、以下となる。

　　　
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 9-C-11式

　　上式 9-C-11 式は、(x₂-x₀) を因子に持つので、下式となる。

　　　　
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 9-C-12式

　　第 2 項の積分 9-C-10 式は、以下の 9-C-13 式となる。分母の括弧内の位置!!

　　　
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 9-C-13式

　　第 3 項の積分は、以下の 9-C-14 式となる。これの算出計算は第 1 項と同じである。

　　　
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　8-C-14式

　　したがって、不均等間隔の離散データを積分する 2 次式による積分計算式は、以下となる。

　　　

　　　　　
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 9-C-15式

　　上記 9-C-15式で、 (x₁-x₀)=(x₂-x₁)=h として、代入すれば、Simpson 1/3 則を得る。

　2)不等間隔の離散データ用 3 次式(Simpson 3/8 則の原形)の算出
　　下記の 4 点を通る

　　　　　　　　　　　　　　　　　　　　　　　　　　9-C-16式

　　Lagrange補間の 3 次式は、下記の 9-C-17式になる。

　　　

　　　　　　
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 9-C-17式

　　　この式を積分すると、3 次式による不均等間隔データの積分方法が得られる事になる。ここでは、式が煩
　　雑感を与えるために、計算の途中経過を省き、結果のみを記載する。

　　上式の y(x) の積分は、

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 9-C-18式

　　で示される。この時に、第一項の積分は、

　　　

　　　　　
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 9-C-19式

　　となる。第二項は、以下となる。

　　　
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 9-C-20式

　　第三項は、第二項と類似の式となり、以下となる。

　　　
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 9-C-21式

　　第四項は、第一項と類似の式となり、以下となる。

　　　

　　　　　
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 9-C-22式

　　　第一項から第四項までの結果を合算すると、不均等間隔の離散データを積分する 3 次式による積分計算
　　式が得られる事になる。これらの結果の式で、 (x₁ - x₀) 等を h と置き、代入すると、Simpson3/8 則とな
　　るはずである。これは、下記の数値計算による検証で確認できる。

2、不等間隔用計算式の検証　(コード 2 )
　　二次式(二次積分式)、三次式(三次積分式) の検証を行った。　この検証計算は、以下に示す計算方法である。

　　例えば、上記 9-C-15式は、三点 (x₀ , y₀) , (x₁ , y₁) , (x₂ , y₂) を通る2次式である。

　　　

　　　　　
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 9-C-15式

　今、

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 9-C-23式

　とする。この時に、3 点の x を以下とすると、x に対応した y は以下となる。

　　　

　　　

　9-C-15式の左辺　9-C-16式の [1,4] 区間の定積分は、以下のように 42 となる。.

　　　　　　　　　　　　　　　　　　　　 9-C-24式

　また、9-C-15式の右辺の第一項は、以下のように 0 となる。

　　　　　　　　 9-C-25式

　第二項は、以下のように 18 となる。

　　　　　　　　　　　　　　　　　9-C-26式

　第三項は、24 となる。

　　　　　　　　　9-C-27式

　9-C-25式、-26式、-27式の和 42 (=0+18+24) は、9-C-24式の 42 と同じである。

　　従って、3 点を通る 2 次式の Lagrage 補間式の積分式(等間隔、Simpson1/3 則)、4点を通る 3 次式の
　Lgarange 補間式の積分式(等間隔、Simpson3/8 則）等々は、各点が等間隔あるいは不均等間隔に係らず、
　その次数においては、正確な定積分値を与える計算式である。

　　上記の考えで、検証計算コードは、次数毎に、x の個数とそれぞれの値とｘに対応した y(x) を予め求めて
　置き、その値を積分式に代入する事で、積分値を算出する方法を採った。

　　　　　　　　

このページの先頭へ

不等間隔の離散データ時の Legendre 多項式による級数展開

1、全般的な説明
　　不等間隔のデータの積分は、不等間隔の 2 次式および 3 次式の積分計算式が必要となり、
　上節に示すように、作り出し、計算式の検証を数値計算で行った。

　　しかし、計算式の検証を行ったとは言え、不等間隔の離散データに対する Legendre 多項式による級数展開の
　可否は検証されていないので、Chebyshev 多項式ｔ11 の等間隔の離散データ( 3 節)に対する Legendre多項
　式の級数展開を、同じコード内で計算し、その後に、不等間隔のデータについて、計算を行った。

　　計算対象； [-1,1] 区間、 Chebyshev t11 （11次)、データ数 240、120、60 (等間隔、不等間隔とも)
　　級数展開； Legendre 多項式 11次まで

　　

2、具体的な計算と結果　(コード　3 )
　1)等間隔の離散データのLegendre多項式による級数展開の計算結果
　　 Chebyshev t11 (11次) を[-1,1]区間で、240、120、60に等間隔に分割された離散データを級数展開した。
　　その結果を示す。この計算は、前章の計算結果と比較する事により、不等間隔用の積分式の検証になる。

　　なお、用語として、積分式として記載したのは、Simpson1/3 則等が、扱いやすいように簡易化された計算
　　式であり、その用語を使用すると、等間隔のイメージが残るので、2次積分式のように2次式を積分したイメ
　　ージが生じるような表現とした。

　　　・等間隔 240 分割の計算結果
　　　　台形則を除けば、ほぼ Chevyshev t11 をLegendre多項式で近似できているといえる。

　　　　　

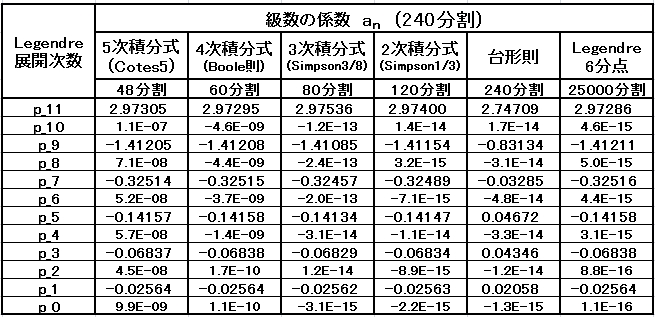
　　　・等間隔 120 分割の計算結果
　　　　計算値は、前章と同じであり、不等間隔用の積分式は正しいと言える。

　　　　　

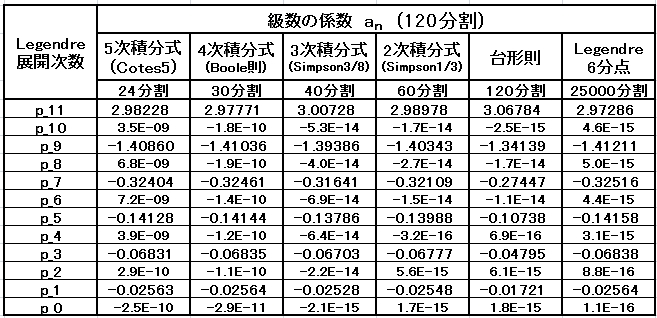
　　　・等間隔 60 分割の計算結果
　　　　60分割では、近似の精度は低くなる。表は表示せず。

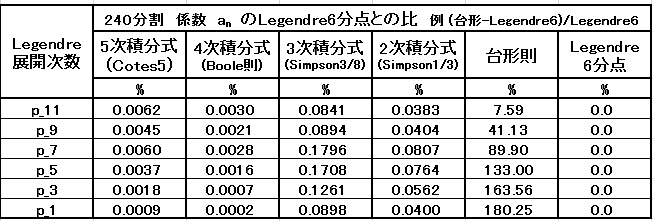
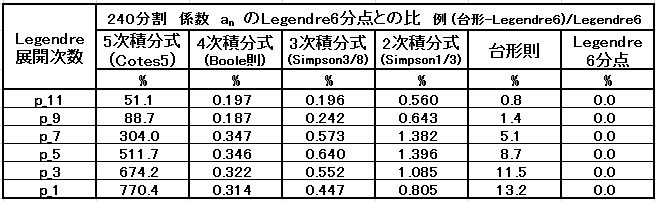
　　　・等間隔 240 分割の Legendre 6 分点法との比較
　　　　近似法として、3次積分式は左程すぐれていない。用途はあるはずである。

　　　　　

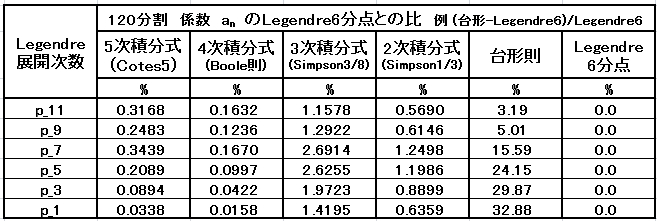
　　　　・等間隔 120 分割の Legendre 6 分点法との比較
　　　　　　

　　　　　

　　　・等間隔 60 分割の Legendre 6 分点法との比較
　　　　

　　　　　

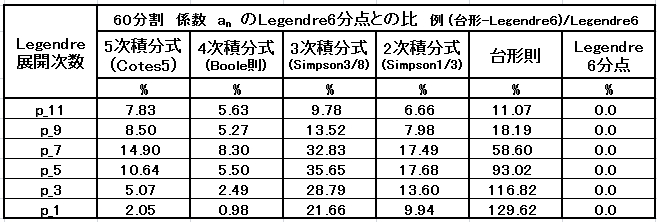
　　　　　結論を言えば、作成した不等間隔用の計算式に誤りはない。

　2)不均等間隔の離散データの生成
　　　等間隔のデータから、最初の 1 個を得て、次のデータを 1 個飛ばし、次のデータを 2 番目のデータとし、
　　更に、次の 2 個のデータを飛ばして得たデータを 3 番目のデータとし、次は、3 個飛ばしの方法で生成した。　

　　　この部分のコードを下記にしめす。下記の p=j+p の部分で、データを不等間隔にする。
　　　例えば、 p=(int)(j+0.8*p)　と p に 0.8 を掛けると飛ばしが緩和される。
　　　　
　　　コード

　　　for(int j=0;j<=kdiv;j++)
　　　{
  　　　　p=j+p;//通過するたびに、pがj+pで増加　注、等間隔の時は消す。
  　　　　x=2.0/kdiv*(j+p)-1.0;// 増加した p+j で x の位置が増加
     　　　　 ・・・
　　　　｝

　　　この計算では、等間隔の分割数 kdiv を予め求め、級数展開の計算を行った。
　　　　・不均等間隔　240 個；ｋdiv=29000 　(等間隔分割、[-1,1] 区間)
　　　　・不均等間隔　120 個；ｋdiv= 7350 　 (等間隔分割、[-1,1] 区間)
　　　　・不均等間隔　 60 個；ｋdiv= 1880 　 (等間隔分割、[-1,1] 区間)

　3)不等間隔の離散データの分布と計算結果
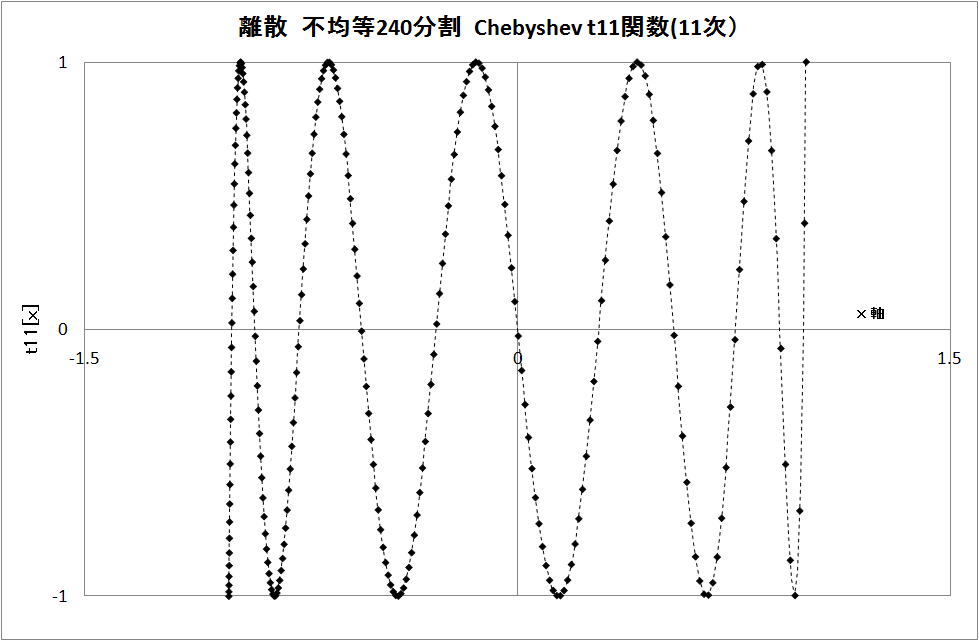
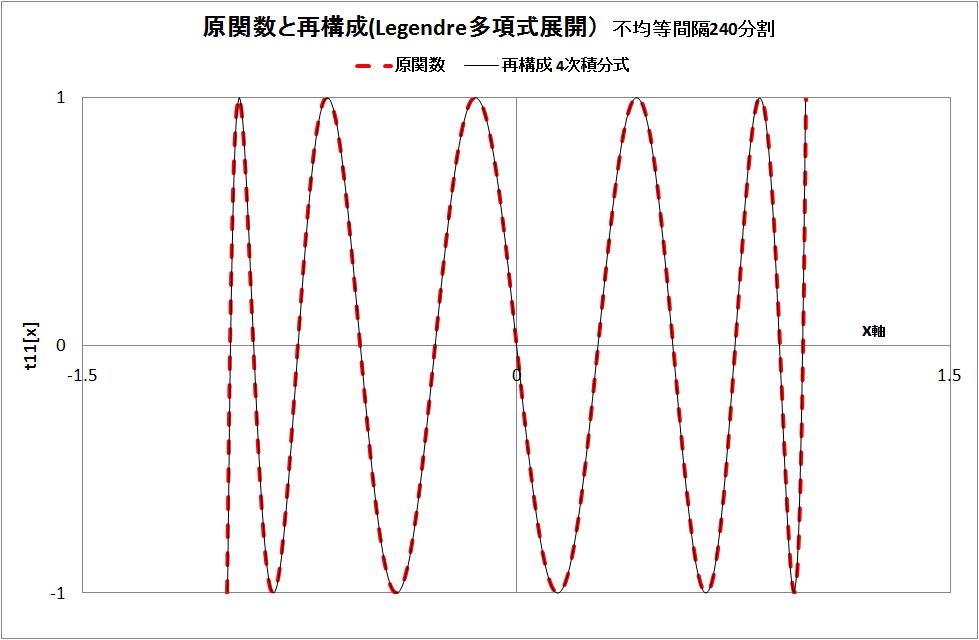
　　(1)不等間隔 240 分割
　　　　・離散データの分布
　　　　　下図に示すように、この不等間隔化計算は、[-1,1]区間の 1 に近づくと計算点が減少する事がわかる。

　　　

　　　　・再構成　4次積分式の係数による図　合致している。

　　　

　　　　・級数展開の係数 an の計算結果
　　　　　

　　　　　

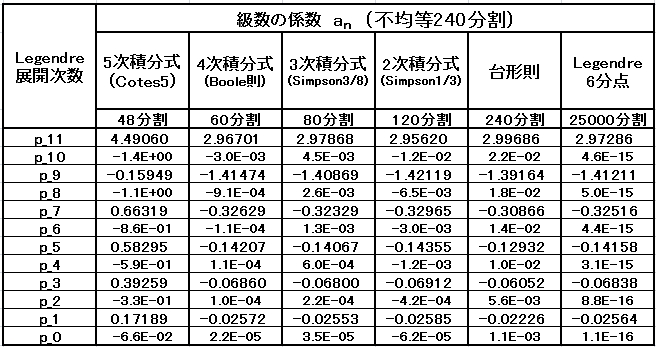
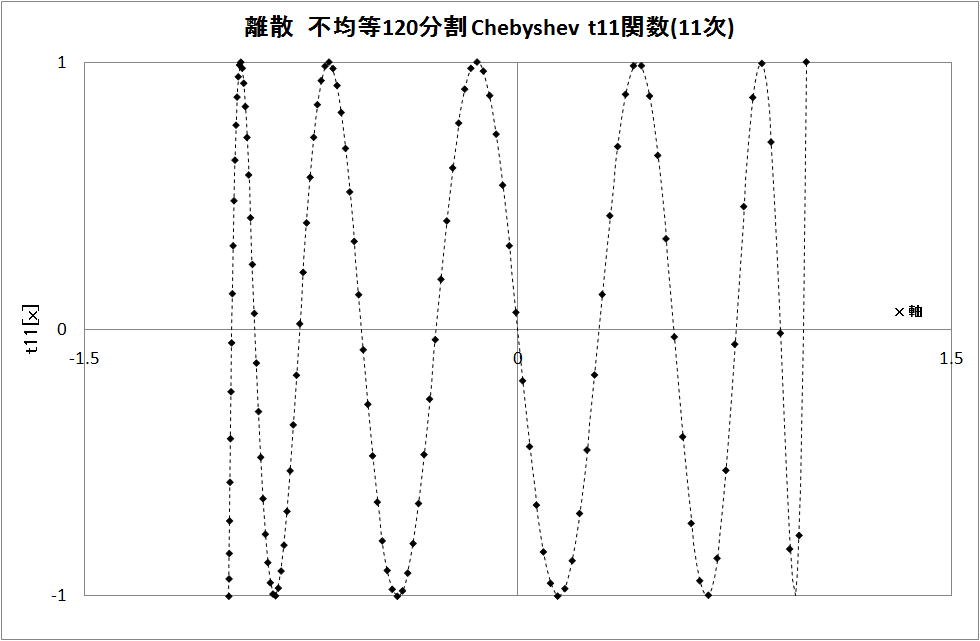
　　(2)不均等間隔 120 分割
　　　　・離散データの分布
　　　　　区間の 1.0 側はデータが少ない。

　　　

　　　　・再構成　

　　　

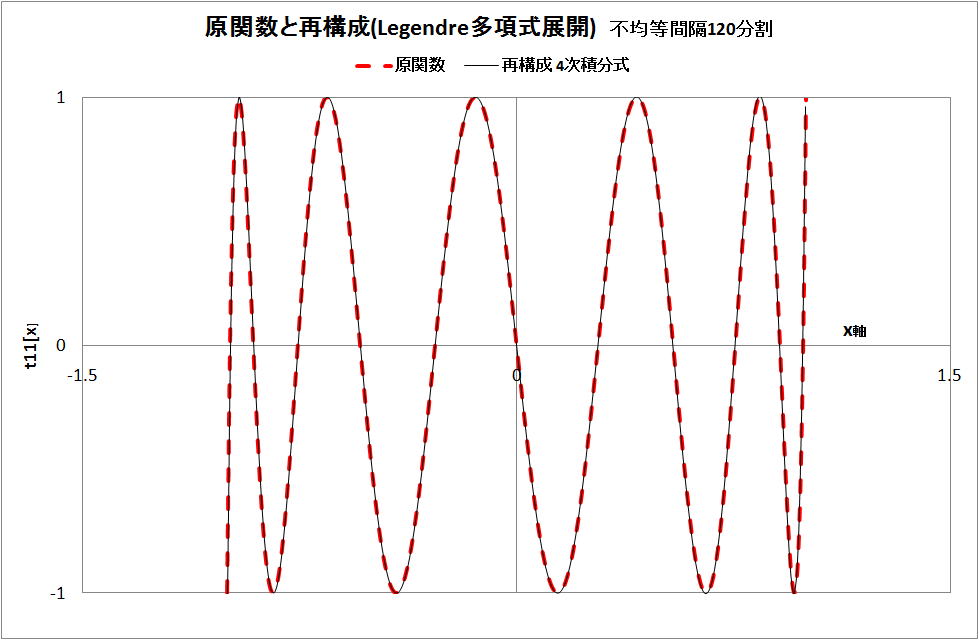
　　　　・級数展開の係数 an の計算結果
　　　　　

　　　　　

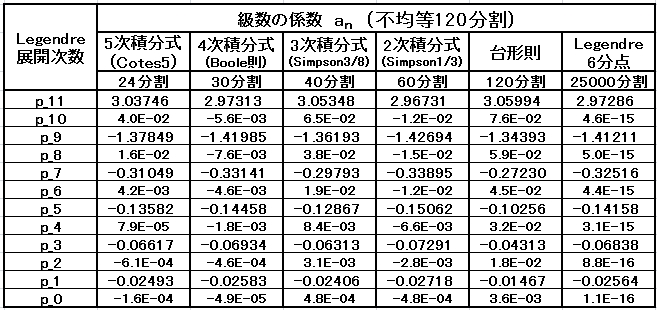
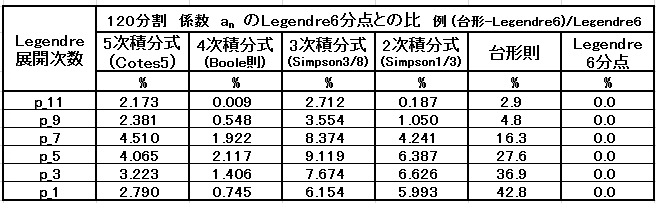
　　3）不均等間隔 60 分割
　　　　・離散データの分布について、全体的にほとんどデータがない。

　　　

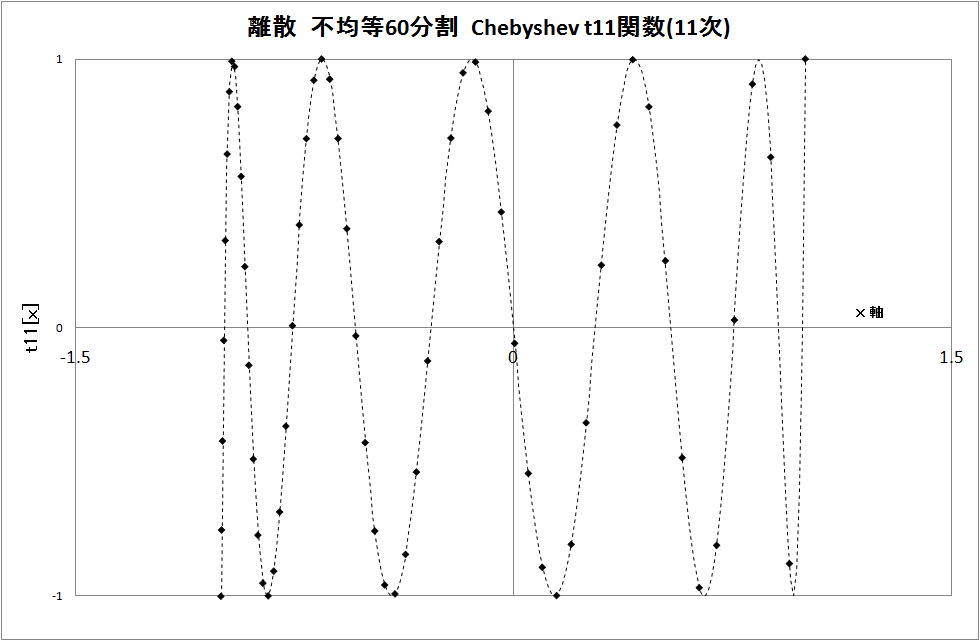
　　　　・再構成　

　　　

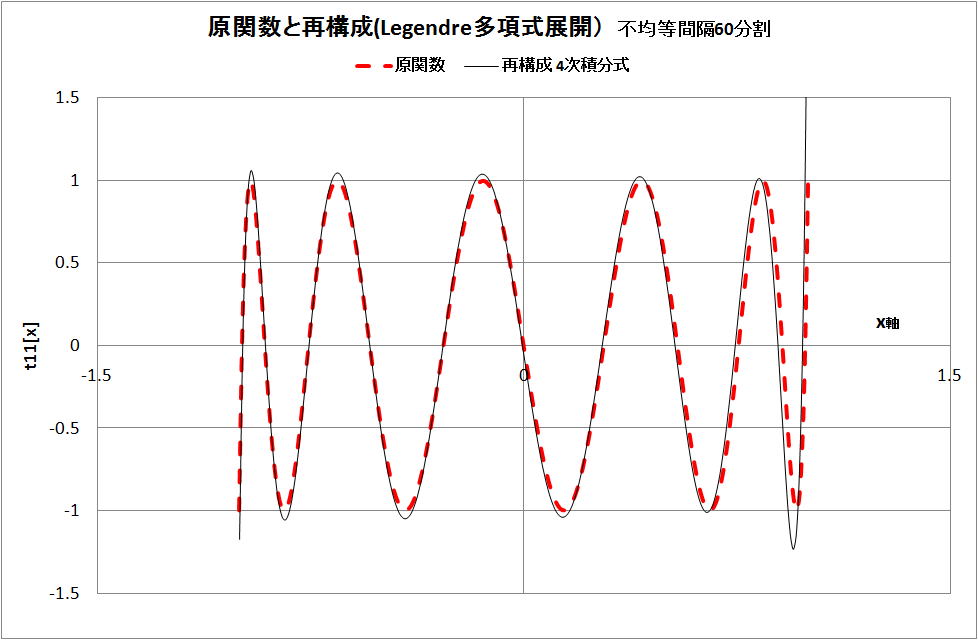
　　　　　　・級数展開の係数 an の計算結果
　　　　　　　

　　　　　

3、結論　今回の不等間隔のデータからは、120分割以上あれば、級数展開出来ると考える。
　　　　　

　　　　　　　　

このページの先頭へ

Information

2012年: この章の全体履歴
2012年1月　
2012、2013年: この章の変更追加履歴
6)花、日本の大通りの画像追加 2013/9/30
5)新宿御苑、Skytreeの画像追加 2013/9/28
4)不等間隔の離散データ時の多項式級数展開(現在3次まで)記載 2012/4/3
3)多次数の積分式の検証コード(現在3次まで）記載 2012/4/1
2)級数展開の計算結果の説明記載 2012/4/1
1)等間隔、不等間隔データの説明記載 2012/3/31

このページの先頭へ

_________________________＿＿＿＿__＿＿____＿＿_______計算コードの具体例______________________________________________
1、等間隔の離散データの数値積分 (コード 1 )
#include <fstream>
#include <vector>
#include <iomanip>
#include <numeric>
using namespace std;

vector<double> Legendre_function();

//Legendre多項式による級数展開
int main()
{
vector<double>hx;
hx=Legendre_function();
hx.resize(hx.size());

vector<double>g_f(121,0.0);
g_f[0]=-1.0;g_f[1]=0.426228563;
g_f[2]=0.957249993;g_f[3]=0.938832493;
g_f[4]=0.623413436;g_f[5]=0.188733683;
g_f[6]=-0.246343772;g_f[7]=-0.608508732;
g_f[8]=-0.85887752;g_f[9]=-0.983796405;
g_f[10]=-0.987329732;g_f[11]=-0.88521039;
g_f[12]=-0.700051374;g_f[13]=-0.457636969;
g_f[14]=-0.1841305;g_f[15]=0.095947266;
g_f[16]=0.361099065;g_f[17]=0.593706675;
g_f[18]=0.780462664;g_f[19]=0.912467411;
g_f[20]=0.985068898;g_f[21]=0.997512181;
g_f[22]=0.952455815;g_f[23]=0.855403646;
g_f[24]=0.714092483;g_f[25]=0.537868881;
g_f[26]=0.337081887;g_f[27]=0.122512747;
g_f[28]=-0.09514249;g_f[29]=-0.305726087;
g_f[30]=-0.5;g_f[31]=-0.669951479;
g_f[32]=-0.809021794;g_f[33]=-0.912259409;
g_f[34]=-0.976401004;g_f[35]=-0.999885381;
g_f[36]=-0.982806569;g_f[37]=-0.926813444;
g_f[38]=-0.834963819;g_f[39]=-0.711541395;
g_f[40]=-0.561844118;g_f[41]=-0.391952451;
g_f[42]=-0.208485857;g_f[43]=-0.018355398;
g_f[44]=0.171480172;g_f[45]=0.354248047;
g_f[46]=0.523578726;g_f[47]=0.673701833;
g_f[48]=0.79961602;g_f[49]=0.897229444;
g_f[50]=0.963468193;g_f[51]=0.996350971;
g_f[52]=0.995029208;g_f[53]=0.959792638;
g_f[54]=0.892041206;g_f[55]=0.794224939;
g_f[56]=0.669754127;g_f[57]=0.522882805;
g_f[58]=0.358569089;g_f[59]=0.182316398;
g_f[60]=0.0;g_f[61]=-0.182316398;
g_f[62]=-0.358569089;g_f[63]=-0.522882805;
g_f[64]=-0.669754127;g_f[65]=-0.794224939;
g_f[66]=-0.892041206;g_f[67]=-0.959792638;
g_f[68]=-0.995029208;g_f[69]=-0.996350971;
g_f[70]=-0.963468193;g_f[71]=-0.897229444;
g_f[72]=-0.79961602;g_f[73]=-0.673701833;
g_f[74]=-0.523578726;g_f[75]=-0.354248047;
g_f[76]=-0.171480172;g_f[77]=0.018355398;
g_f[78]=0.208485857;g_f[79]=0.391952451;
g_f[80]=0.561844118;g_f[81]=0.711541395;
g_f[82]=0.834963819;g_f[83]=0.926813444;
g_f[84]=0.982806569;g_f[85]=0.999885381;
g_f[86]=0.976401004;g_f[87]=0.912259409;
g_f[88]=0.809021794;g_f[89]=0.669951479;
g_f[90]=0.5;g_f[91]=0.305726087;
g_f[92]=0.09514249;g_f[93]=-0.122512747;
g_f[94]=-0.337081887;g_f[95]=-0.537868881;
g_f[96]=-0.714092483;g_f[97]=-0.855403646;
g_f[98]=-0.952455815;g_f[99]=-0.997512181;
g_f[100]=-0.985068898;g_f[101]=-0.912467411;
g_f[102]=-0.780462664;g_f[103]=-0.593706675;
g_f[104]=-0.361099065;g_f[105]=-0.095947266;
g_f[106]=0.1841305;g_f[107]=0.457636969;
g_f[108]=0.700051374;g_f[109]=0.88521039;
g_f[110]=0.987329732;g_f[111]=0.983796405;
g_f[112]=0.85887752;g_f[113]=0.608508732;
g_f[114]=0.246343772;g_f[115]=-0.188733683;
g_f[116]=-0.623413436;g_f[117]=-0.938832493;
g_f[118]=-0.957249993;g_f[119]=-0.426228563;
g_f[120]=1.0;

vector<int>div0(1,0);
//div0[0]=120;
//div0[0]=60;
div0[0]=40;
//div0[0]=30;

double x0=-1.0;
double x1=1.0;

for(int i=0;i<(int)div0.size();i++)
{
int div=div0[i];
vector<long double>fx;
int ak=11;
vector<long double>tr_an(ak+1,0.0),s3_an(ak+1,0.0);
vector<long double>s8_an(ak+1,0.0),b2_an(ak+1,0.0);

for(int L=ak;L>=0;L--)
{
fx.clear();
int m=L;
for(int i=L*(L+1)/2;i<m+L*(L+1)/2+1;i++)fx.push_back(hx[i]);
fx.resize(fx.size());

double factor=(2.0*L+1)/2.0;

double h=(x1-x0)/div;
double f_xn0=0.0;//分割始点
double f_xn2=0.0;//幅の1/4点
double f_xn3=0.0;//幅の1/3点
double f_xnm=0.0;//中間点
double f_xn6=0.0;//幅の2/3点
double f_xn7=0.0;//幅の3/4点
double f_xn1=0.0;//終点

double g_xn0=0.0;//分割始点
double g_xn2=0.0;//幅の1/4点
double g_xn3=0.0;//幅の1/3点
double g_xnm=0.0;//中間点
double g_xn6=0.0;//幅の2/3点
double g_xn7=0.0;//幅の3/4点
double g_xn1=0.0;//終点

double fg_xn0=0.0;
double fg_xnm=0.0;
double fg_xn1=0.0;

double tr_ort=0.0;// trapezoid 台形則
double s3_ort=0.0;// simpson　1/3則
double s8_ort=0.0;// simpson　3/8則
double b2_ort=0.0;// Boole則 2/45

for(int j=0;j<div;j++)
{
vector<double>p_xn0(m+1,0.0);
vector<double>p_xn2(m+1,0.0);
vector<double>p_xn3(m+1,0.0);
vector<double>p_xnm(m+1,0.0);
vector<double>p_xn6(m+1,0.0);
vector<double>p_xn7(m+1,0.0);
vector<double>p_xn1(m+1,0.0);

for(int i=0;i<m+1;i++)
{
p_xn0[i]=pow(x0+j*h,i);
p_xn2[i]=pow(x0+j*h+h/4.0,i);
p_xn3[i]=pow(x0+j*h+h/3.0,i);
p_xnm[i]=pow(x0+j*h+h/2.0,i);
p_xn6[i]=pow(x0+j*h+2.0*h/3.0,i);
p_xn7[i]=pow(x0+j*h+3.0*h/4.0,i);
p_xn1[i]=pow(x0+j*h+h,i);
}

f_xn0=inner_product(fx.begin(),fx.end(),p_xn0.begin(),0.0,plus<double>(),multiplies<double>());
f_xn2=inner_product(fx.begin(),fx.end(),p_xn2.begin(),0.0,plus<double>(),multiplies<double>());
f_xn3=inner_product(fx.begin(),fx.end(),p_xn3.begin(),0.0,plus<double>(),multiplies<double>());
f_xnm=inner_product(fx.begin(),fx.end(),p_xnm.begin(),0.0,plus<double>(),multiplies<double>());
f_xn6=inner_product(fx.begin(),fx.end(),p_xn6.begin(),0.0,plus<double>(),multiplies<double>());
f_xn7=inner_product(fx.begin(),fx.end(),p_xn7.begin(),0.0,plus<double>(),multiplies<double>());
f_xn1=inner_product(fx.begin(),fx.end(),p_xn1.begin(),0.0,plus<double>(),multiplies<double>());

/*
// div0[0]=120
g_xn0=g_f[j+0];
g_xn1=g_f[j+1];
fg_xn0=f_xn0*g_xn0;
fg_xn1=f_xn1*g_xn1;
tr_ort=tr_ort+(fg_xn0+fg_xn1)*h/2.0;

// div0[0]=60
g_xn0=g_f[2*j+0];
g_xnm=g_f[2*j+1];
g_xn1=g_f[2*j+2];
fg_xn0=f_xn0*g_xn0;
fg_xnm=f_xnm*g_xnm;
fg_xn1=f_xn1*g_xn1;
tr_ort=tr_ort+(fg_xn0+fg_xn1)*h/2.0;
s3_ort=s3_ort+(fg_xn0+4.0*fg_xnm+fg_xn1)/3.0*h/2.0;
*/

// div0[0]=40
g_xn0=g_f[3*j+0];
g_xn3=g_f[3*j+1];
g_xn6=g_f[3*j+2];
g_xn1=g_f[3*j+3];
fg_xn0=f_xn0*g_xn0;
fg_xn1=f_xn1*g_xn1;
tr_ort=tr_ort+(fg_xn0+fg_xn1)*h/2.0;
s8_ort=s8_ort+(fg_xn0+3.0*f_xn3*g_xn3+3.0*f_xn6*g_xn6+
fg_xn1)*3.0/8.0*h/3.0;

/*
// div0[0]=30
g_xn0=g_f[4*j+0];
g_xn2=g_f[4*j+1];
g_xnm=g_f[4*j+2];
g_xn7=g_f[4*j+3];
g_xn1=g_f[4*j+4];
fg_xn0=f_xn0*g_xn0;
fg_xnm=f_xnm*g_xnm;
fg_xn1=f_xn1*g_xn1;
tr_ort=tr_ort+(fg_xn0+fg_xn1)*h/2.0;
s3_ort=s3_ort+(fg_xn0+4.0*fg_xnm+fg_xn1)/3.0*h/2.0;
b2_ort=b2_ort+(7.0*fg_xn0+32.0*f_xn2*g_xn2+12.0*fg_xnm+32.0*f_xn7*g_xn7+7.0*fg_xn1)*2.0/45.0*h/4.0;
*/

}//div

tr_an[L]=tr_ort*factor;
s3_an[L]=s3_ort*factor;
s8_an[L]=s8_ort*factor;
b2_an[L]=b2_ort*factor;

}//fx

fstream out00an("An_Legngrepoly.csv",ios::out |ios::binary |ios::app);
out00an<<"p_"<<"L"<<","<<"div"<<","<<"tr_an[L]"<<","<<"s3_an[L]"<<","<<"s8_an[L]"<<","<<"b2_an[L]"<<endl;
for(int L=ak;L>=0;L--) out00an<<"p_"<<L<<","<<div<<","<<setprecision(20)<<tr_an[L]<<","<<s3_an[L]<<","<<s8_an[L]<<","<<b2_an[L]<<endl;
out00an<<" "<<endl;
out00an.close();

}// div0[i]

return 0;
}

vector<double> Legendre_function()
{
//Legendre関数p　
vector<double >p0(0+1,0.0);
p0[0]=1.0;

vector<double >p1(1+1,0.0);
p1[0]=0.0;
p1[1]=1.0;

vector<double >p2(2+1,0.0);
p2[0]=-1/2.0;
p2[1]=0.0;
p2[2]=3/2.0;

vector<double >p3(3+1,0.0);
p3[0]=0.0;
p3[1]=-3/2.0;
p3[2]=0.0;
p3[3]=5/2.0;

vector<double >p4(4+1,0.0);
p4[0]=3/8.0;
p4[1]=0.0;
p4[2]=-30/8.0;
p4[3]=0.0;
p4[4]=35/8.0;

vector<double >p5(5+1,0.0);
p5[0]=0.0;
p5[1]=15.0/8.0;
p5[2]=0.0;
p5[3]=-70.0/8.0;
p5[4]=0.0;
p5[5]=63.0/8.0;

vector<double >p6(6+1,0.0);
p6[0]=-5.0/16.0;
p6[1]=0.0;
p6[2]=105.0/16.0;
p6[3]=0.0;
p6[4]=-315.0/16.0;
p6[5]=0.0;
p6[6]=231.0/16.0;

vector<double>p7(7+1,0.0);
p7[0]=0.0;
p7[1]=-35/16.0;
p7[2]=0.0;
p7[3]=315/16.0;
p7[4]=0.0;
p7[5]=-693/16.0;
p7[6]=0.0;
p7[7]=429/16.0;

vector<double>p8(8+1,0.0);
p8[0]=35/128.0;
p8[1]=0.0;
p8[2]=-315/32.0;
p8[3]=0.0;
p8[4]=3465/64.0;
p8[5]=0.0;
p8[6]=-3003/32.0;
p8[7]=0.0;
p8[8]=6435/128.0;

vector<double>p9(9+1,0.0);
p9[0]=0.0;
p9[1]=315/128.0;
p9[2]=0.0;
p9[3]=-1155/32.0;
p9[4]=0.0;
p9[5]=9009/64.0;
p9[6]=0.0;
p9[7]=-6435/32.0;
p9[8]=0.0;
p9[9]=12155/128.0;

vector<double>p10(10+1,0.0);
p10[0]=-63/256.0;
p10[1]=0.0;
p10[2]=3465/256.0;
p10[3]=0.0;
p10[4]=-15015/128.0;
p10[5]=0.0;
p10[6]=45045/128.0;
p10[7]=0.0;
p10[8]=-109395/256.0;
p10[9]=0.0;
p10[10]=46189/256.0;

vector<double>p11(11+1,0.0);
p11[0]=0.0;
p11[1]=-693/256.0;
p11[2]=0.0;
p11[3]=15015/256.0;
p11[4]=0.0;
p11[5]=-45045/128.0;
p11[6]=0.0;
p11[7]=109395/128.0;
p11[8]=0.0;
p11[9]=-230945/256.0;
p11[10]=0.0;
p11[11]=88179/256.0;

int k;
vector<double>hx;
k=0;for(int i=0;i<k+1;i++) hx.push_back(p0[i]);
k=1;for(int i=0;i<k+1;i++) hx.push_back(p1[i]);
k=2;for(int i=0;i<k+1;i++) hx.push_back(p2[i]);
k=3;for(int i=0;i<k+1;i++) hx.push_back(p3[i]);
k=4;for(int i=0;i<k+1;i++) hx.push_back(p4[i]);
k=5;for(int i=0;i<k+1;i++) hx.push_back(p5[i]);
k=6;for(int i=0;i<k+1;i++) hx.push_back(p6[i]);
k=7;for(int i=0;i<k+1;i++) hx.push_back(p7[i]);
k=8;for(int i=0;i<k+1;i++) hx.push_back(p8[i]);
k=9;for(int i=0;i<k+1;i++) hx.push_back(p9[i]);
k=10;for(int i=0;i<k+1;i++) hx.push_back(p10[i]);
k=11;for(int i=0;i<k+1;i++) hx.push_back(p11[i]);
hx.resize(hx.size());

return hx;

}

本章 9 章の説明へ

2、不等間隔の離散データ用 2 次式および 3 次式による積分式の検証計算(コード 2)
#include <fstream>
#include <vector>
#include <iomanip>
#include <numeric>
#include <iostream>
using namespace std;

//不均等あるいは不等間隔の積分式
int main()
{
double x0=-10.0;
double x1=-9.0;
double x2=-7.0;
double x3=-3.0;

// 2x^2
double y20=200.0;
double y21=162.0;
double y22=98.0;
double s1by3_ana=2.0/3.0*(x2*x2*x2-x0*x0*x0);

double s1by3_ir=
+(x2-x0)/(x1-x0)*(3.0*(x1-x0)-(x2-x0))/6.0*y20

+(x2-x0)*(x2-x0)*(x2-x0)/(x2-x1)/(x1-x0)/6.0*y21

+(x2-x0)/(x2-x1)*(3.0*(x2-x1)-(x2-x0))/6.0*y22

;

//2x^3
double y30=-2000.0;
double y31=-1458.0;
double y32=-686.0;
double y33=-54.0;
double s3by8_ana=2.0/4.0*(x3*x3*x3*x3-x0*x0*x0*x0);

double s3by8_ir=
+1.0/12.0*(x3-x0)*(x3*x3-2.0*x3*x1-2.0*x3*x2+2.0*x0*x3+6.0*x1*x2-4.0*x0*x1-4.0*x0*x2+3.0*x0*x0)/(x2-x0)/(x1-x0)*y30

+1.0/12.0*(x3-x0)*(x3-x0)*(x3-x0)*(-x3-x0+2.0*x2)/(x1-x0)/(x2-x1)/(x3-x1)*y31

-1.0/12.0*(x3-x0)*(x3-x0)*(x3-x0)*(-x3+2.0*x1-x0)/(x2-x1)/(x2-x0)/(x3-x2)*y32

+1.0/12.0*(x3-x0)*(3.0*x3*x3-4.0*x3*x1-4.0*x3*x2+2.0*x0*x3+x0*x0-2.0*x1*x0-2.0*x2*x0+6.0*x1*x2)/(x3-x2)/(x3-x1)*y33

;



// 以下の検証計算は順次記載していく。　　
 


  

// 以上の検証計算は順次記載していく。






return 0;

}





    本章 9 章の説明へ

    
                        

    

    

    3、不等間隔の離散データ時の Legendree 多項式による級数展開 ( コード 3 )
#include <cmath>

#include <fstream>

#include <vector>

#include <numeric>

#include <iostream>

using namespace std;



vector<double> Legendre_function();



//不等間隔&等間隔　Legendre多項式による級数展開

int main()

{



vector<double>hx;

hx=Legendre_function();

hx.resize(hx.size());



vector<long double>t11(11+1,0.0);

t11[0]=0.0;

t11[1]=-11.0;

t11[2]=0.0;

t11[3]=220.0;

t11[4]=0.0;

t11[5]=-1232;

t11[6]=0.0;

t11[7]=2816.0;

t11[8]=0.0;

t11[9]=-2816.0;

t11[10]=0.0;

t11[11]=1024.0;



vector<long double>xn(t11.size(),0.0);

long double x=0.0;





int kdiv=29000;// 不均等240分割

//int kdiv=7350;// 不均等120分割

//int kdiv=1880;// 不均等60分割



//int kdiv=240;// 等間隔240分割

//int kdiv=120;//等間隔120分割

//int kdiv=120;// 等間隔60分割



vector<double>g_x;

vector<double>g_f;



int p=0;



for(int j=0;j<=kdiv;j++)

{

	p=j+p;//通過するたびに、pがj+pで増加　　

	x=2.0/kdiv*(j+p)-1.0;// 増加した p+j で x の位置が増加 	



	if(x<=1.0001)

	{

		g_x.push_back(x);

	    for(int jj=0;jj<(int)t11.size();jj++)

			{

				xn[jj]=pow(x,(long double)jj);

		}

	    double c=inner_product(t11.begin(),t11.end(),xn.begin(),0.0,plus<long double>(),multiplies<long double>());	

	    g_f.push_back(c);

	}

}

g_x.push_back(1.0);//等間隔の時は、消す。

g_f.push_back(1.0);//等間隔の時は、消す。



g_x.resize(g_x.size());

g_f.resize(g_f.size());



fstream outChebyt11("240_t11.csv",ios::out|ios::binary);

//fstream outChebyt11("120_t11.csv",ios::out|ios::binary);

//fstream outChebyt11("60_t11.csv",ios::out|ios::binary);

for(int j=0;j<(int)g_x.size();j++) 

	{

		outChebyt11<<j<<","<<g_x[j]<<","<<g_f[j]<<endl;

}

outChebyt11.close();





//int div=(int)g_x.size()-1,parameter=1;//台形用

//int div=(int)g_x.size()/2,parameter=2;//台+s3

//int div=(int)g_x.size()/3, parameter=3;//台+s8

//int div=(int)g_x.size()/4, parameter=4;//台+s3+b2

int div=(int)g_x.size()/5, parameter=5;//台+k5



vector<long double>fx;



int ak=11;

vector<long double>tr_an(ak+1,0.0),s3_an(ak+1,0.0);

vector<long double>s8_an(ak+1,0.0),b2_an(ak+1,0.0);

vector<long double>k5_an(ak+1,0.0);// ｋ5は5次式



for(int L=ak;L>=0;L--)

{

fx.clear();

int m=L;

for(int i=L*(L+1)/2;i<m+L*(L+1)/2+1;i++) fx.push_back(hx[i]);

fx.resize(fx.size());



double factor=(2.0*L+1)/2.0;



double f_xn00=0.0;//分割始点

double f_xn20=0.0;//幅の1/5点

double f_xn25=0.0;//幅の1/4点

double f_xn33=0.0;//幅の1/3点

double f_xn40=0.0;//幅の2/5点

double f_xn50=0.0;//中間点

double f_xn60=0.0;//幅の3/5点

double f_xn66=0.0;//幅の2/3点

double f_xn75=0.0;//幅の3/4点

double f_xn80=0.0;//幅の4/5点

double f_xned=0.0;//終点



double g_xn00=0.0;//分割始点

double g_xn20=0.0;//幅の1/5点

double g_xn25=0.0;//幅の1/4点

double g_xn33=0.0;//幅の1/3点

double g_xn40=0.0;//幅の2/5点

double g_xn50=0.0;//中間点

double g_xn60=0.0;//幅の3/5点

double g_xn66=0.0;//幅の2/3点

double g_xn75=0.0;//幅の3/4点

double g_xn80=0.0;//幅の4/5点

double g_xned=0.0;//終点



double tr_ort=0.0;// trapezoid 台形則

double s3_ort=0.0;// simpson　1/3則 

double s8_ort=0.0;// simpson　3/8則

double b2_ort=0.0;// Boole則 2/45

double k5_ort=0.0;// Cotes5次





for(int j=0;j<div;j++)

{ 

 vector<double>p_xn00(m+1,0.0);

 vector<double>p_xn20(m+1,0.0);

 vector<double>p_xn25(m+1,0.0);

 vector<double>p_xn33(m+1,0.0);

 vector<double>p_xn40(m+1,0.0);

 vector<double>p_xn50(m+1,0.0);

 vector<double>p_xn60(m+1,0.0);

 vector<double>p_xn66(m+1,0.0);

 vector<double>p_xn75(m+1,0.0);

 vector<double>p_xn80(m+1,0.0);

 vector<double>p_xned(m+1,0.0);





if(parameter==1)

{

// 台形則       

 for(int i=0;i<m+1;i++)

 {

	

	 p_xn00[i]=pow(g_x[j],i);

	 p_xned[i]=pow(g_x[j+1],i);

	

 }



 f_xn00=inner_product(fx.begin(),fx.end(),p_xn00.begin(),0.0, plus<double>(),multiplies<double>());

 f_xned=inner_product(fx.begin(),fx.end(),p_xned.begin(),0.0, plus<double>(),multiplies<double>()); 



 g_xn00=g_f[1*j+0];

 g_xned=g_f[1*j+1];  



 tr_ort=tr_ort+(f_xn00*g_xn00+f_xned*g_xned)*(g_x[j+1]-g_x[j])/2.0;

}





if(parameter==2)

{

 // 台形則、simpson1/3則 

  for(int i=0;i<m+1;i++)

 {	

	 p_xn00[i]=pow(g_x[2*j+0],i);

	 p_xn50[i]=pow(g_x[2*j+1],i);

	 p_xned[i]=pow(g_x[2*j+2],i);	

 }



 f_xn00=inner_product(fx.begin(),fx.end(),p_xn00.begin(),0.0, plus<double>(),multiplies<double>());

 f_xn50=inner_product(fx.begin(),fx.end(),p_xn50.begin(),0.0, plus<double>(),multiplies<double>());

 f_xned=inner_product(fx.begin(),fx.end(),p_xned.begin(),0.0, plus<double>(),multiplies<double>());

 

 

 g_xn00=g_f[2*j+0];

 g_xn50=g_f[2*j+1];

 g_xned=g_f[2*j+2]; 



 double x0=g_x[2*j+0];

 double x1=g_x[2*j+1];

 double x2=g_x[2*j+2];



 tr_ort=tr_ort+(f_xn00*g_xn00+f_xned*g_xned)*(g_x[2*j+2]-g_x[2*j])/2.0;



 s3_ort=s3_ort+(x2-x0)/(x1-x0)*(3.0*(x1-x0)-(x2-x0))/6.0*f_xn00*g_xn00

	    +(x2-x0)*(x2-x0)*(x2-x0)/(x2-x1)/(x1-x0)/6.0*f_xn50*g_xn50

		+(x2-x0)/(x2-x1)*(3.0*(x2-x1)-(x2-x0))/6.0*f_xned*g_xned; 

}





if(parameter==3)

{

//台形則、simpson3/8則

 for(int i=0;i<m+1;i++)

 {

	 p_xn00[i]=pow(g_x[3*j+0],i);	

     p_xn33[i]=pow(g_x[3*j+1],i);

	 p_xn66[i]=pow(g_x[3*j+2],i);

     p_xned[i]=pow(g_x[3*j+3],i);

 }





 f_xn00=inner_product(fx.begin(),fx.end(),p_xn00.begin(),0.0, plus<double>(),multiplies<double>());

 f_xn33=inner_product(fx.begin(),fx.end(),p_xn33.begin(),0.0, plus<double>(),multiplies<double>());

 f_xn66=inner_product(fx.begin(),fx.end(),p_xn66.begin(),0.0, plus<double>(),multiplies<double>());

 f_xned=inner_product(fx.begin(),fx.end(),p_xned.begin(),0.0, plus<double>(),multiplies<double>());



 

 g_xn00=g_f[3*j+0];

 g_xn33=g_f[3*j+1];

 g_xn66=g_f[3*j+2];

 g_xned=g_f[3*j+3];



 double x0=g_x[3*j+0];

 double x1=g_x[3*j+1];

 double x2=g_x[3*j+2];

 double x3=g_x[3*j+3]; 



 tr_ort=tr_ort+(f_xn00*g_xn00+f_xned*g_xned)*(g_x[3*j+3]-g_x[3*j+0])/2.0;



 s8_ort=s8_ort

	+1.0/12.0*(x3-x0)*(x3*x3-2.0*x3*x1-2.0*x3*x2+2.0*x0*x3+6.0*x1*x2-4.0*x0*x1-4.0*x0*x2+3.0*x0*x0)/(x2-x0)/(x1-x0)*f_xn00*g_xn00

	+1.0/12.0*(x3-x0)*(x3-x0)*(x3-x0)*(-x3-x0+2.0*x2)/(x1-x0)/(x2-x1)/(x3-x1)*f_xn33*g_xn33

	-1.0/12.0*(x3-x0)*(x3-x0)*(x3-x0)*(-x3+2.0*x1-x0)/(x2-x1)/(x2-x0)/(x3-x2)*f_xn66*g_xn66

	+1.0/12.0*(x3-x0)*(3.0*x3*x3-4.0*x3*x1-4.0*x3*x2+2.0*x0*x3+x0*x0-2.0*x1*x0-2.0*x2*x0+6.0*x1*x2)/(x3-x2)/(x3-x1)*f_xned*g_xned;

}



//　以下　後日　記載する。



    

// 以上 後日　記載する。 

	

}	

 

}//div



cout<<"p_"<<L<<","<<div<<endl;



tr_an[L]=tr_ort*factor;

s3_an[L]=s3_ort*factor;  

s8_an[L]=s8_ort*factor;

b2_an[L]=b2_ort*factor;

k5_an[L]=k5_ort*factor;



}//fx



fstream out00an("240_an.csv",ios::out|ios::binary|ios::app);

//fstream out00an("120_an.csv",ios::out|ios::binary|ios::app);

//fstream out00an("60_an.csv",ios::out|ios::binary|ios::app);

out00an<<"p_"<<"L"<<","<<"div"<<","<<"k5_an[L]"<<","<<"b2_an[L]"<<","<<"s8_an[L]"<<","<<"s3_an[L]"<<","<<"tr_an[L]"<<endl;

for(int L=ak;L>=0;L--) out00an<<"p_"<<L<<","<<div<<","<<k5_an[L]<<","<<b2_an[L]<<","<<s8_an[L]<<","<<s3_an[L]<<","<<tr_an[L]<<endl;

out00an<<" "<<endl;

out00an.close();



g_x.clear();

g_f.clear();



int kk=200+1;



vector<long double>re_k5(kk,0.0);

vector<long double>re_b2(kk,0.0);

vector<long double>re_s8(kk,0.0);

vector<long double>re_s3(kk,0.0);

vector<long double>re_tr(kk,0.0);



for(int j=0;j<kk;j++)

{

	x=0.01*j-1.0;

	for(int jj=0;jj<(int)t11.size();jj++) 

		{

			xn[jj]=pow(x,(long double)jj);

	}

  double c=inner_product(t11.begin(),t11.end(),xn.begin(),0.0,plus<long double>(),multiplies<long double>());	

  g_f.push_back(c);

	

	long double k5_sum=0.0,b2_sum=0.0,s8_sum=0.0;

	long double s3_sum=0.0,tr_sum=0.0;



	for(int L=ak;L>=0;L--)

    {

     fx.clear();

     int m=L;

     for(int i=L*(L+1)/2;i<m+L*(L+1)/2+1;i++)fx.push_back(hx[i]);

     fx.resize(fx.size());	

	 for(int i=0;i<m+1;i++) 

		{

			k5_sum=k5_sum+k5_an[L]*fx[i]*pow(x,i);

			b2_sum=b2_sum+b2_an[L]*fx[i]*pow(x,i);

			s8_sum=s8_sum+s8_an[L]*fx[i]*pow(x,i);

			s3_sum=s3_sum+s3_an[L]*fx[i]*pow(x,i);

			tr_sum=tr_sum+tr_an[L]*fx[i]*pow(x,i);

	    }

	}

	re_k5[j]=k5_sum;

	re_b2[j]=b2_sum;

	re_s8[j]=s8_sum;

	re_s3[j]=s3_sum;

	re_tr[j]=tr_sum;

}



fstream outrecalc("240_Recal.csv",ios::out|ios::binary|ios::app);

//fstream outrecalc("120_Recal.csv",ios::out|ios::binary|ios::app);

//fstream outrecalc("60_Recal.csv",ios::out|ios::binary|ios::app);

outrecalc<<"div"<<","<<"j"<<","<<"0.01*j-1."<<","<<"re_k5[j]"<<","<<"re_b2[j]"<<","<<"re_s8[j]"<<","<<"re_s3[j]"<<","<<"re_tr[j]"

<<","<<"g_f[j]"<<","<<"g_f-re_k5"<<","<<"g_f-re_b2"<<","<<"g_f-re_s8"<<","<<"g_f-re_s3"<<","<<"g_f-re_tr"<<endl;



for(int j=0;j<kk;j++)outrecalc<<div<<","<<j<<","<<0.01*j-1.00<<","<<re_k5[j]<<","<<re_b2[j]<<","<<re_s8[j]<<","<<re_s3[j]<<","

    <<re_tr[j]<<","<<g_f[j]<<","<<g_f[j]-re_k5[j]<<","<<g_f[j]-re_b2[j]<<","<<g_f[j]-re_s8[j]<<","<<g_f[j]-re_s3[j]<<","

    <<g_f[j]-re_tr[j]<<endl;

outrecalc<<" "<<endl;

outrecalc.close();



re_k5.clear();

re_b2.clear();

re_s8.clear();

re_s3.clear();

re_tr.clear();



return 0;

}



vector<double> Legendre_function()

{

//Legendre関数p　

vector<double >p0(0+1,0.0);

p0[0]=1.0;



vector<double >p1(1+1,0.0);

p1[0]=0.0;

p1[1]=1.0;



vector<double >p2(2+1,0.0);

p2[0]=-1/2.0;

p2[1]=0.0;

p2[2]=3/2.0;



vector<double >p3(3+1,0.0);

p3[0]=0.0;

p3[1]=-3/2.0;

p3[2]=0.0;

p3[3]=5/2.0;



vector<double >p4(4+1,0.0);

p4[0]=3/8.0;

p4[1]=0.0;

p4[2]=-30/8.0;

p4[3]=0.0;

p4[4]=35/8.0;



vector<double >p5(5+1,0.0);

p5[0]=0.0;

p5[1]=15.0/8.0;

p5[2]=0.0;

p5[3]=-70.0/8.0;

p5[4]=0.0;

p5[5]=63.0/8.0;



vector<double >p6(6+1,0.0);

p6[0]=-5.0/16.0;

p6[1]=0.0;

p6[2]=105.0/16.0;

p6[3]=0.0;

p6[4]=-315.0/16.0;

p6[5]=0.0;

p6[6]=231.0/16.0;	



vector<double>p7(7+1,0.0);

p7[0]=0.0;

p7[1]=-35/16.0;

p7[2]=0.0;

p7[3]=315/16.0;

p7[4]=0.0;

p7[5]=-693/16.0;

p7[6]=0.0;

p7[7]=429/16.0;



vector<double>p8(8+1,0.0);

p8[0]=35/128.0;

p8[1]=0.0;

p8[2]=-315/32.0;

p8[3]=0.0;

p8[4]=3465/64.0;

p8[5]=0.0;

p8[6]=-3003/32.0;

p8[7]=0.0;

p8[8]=6435/128.0;



vector<double>p9(9+1,0.0);

p9[0]=0.0;

p9[1]=315/128.0;

p9[2]=0.0;

p9[3]=-1155/32.0;

p9[4]=0.0;

p9[5]=9009/64.0;

p9[6]=0.0;

p9[7]=-6435/32.0;

p9[8]=0.0;

p9[9]=12155/128.0;



vector<double>p10(10+1,0.0);

p10[0]=-63/256.0;

p10[1]=0.0;

p10[2]=3465/256.0;

p10[3]=0.0;

p10[4]=-15015/128.0;

p10[5]=0.0;

p10[6]=45045/128.0;

p10[7]=0.0;

p10[8]=-109395/256.0;

p10[9]=0.0;

p10[10]=46189/256.0;



vector<double>p11(11+1,0.0);

p11[0]=0.0;

p11[1]=-693/256.0;

p11[2]=0.0;

p11[3]=15015/256.0;

p11[4]=0.0;

p11[5]=-45045/128.0;

p11[6]=0.0;

p11[7]=109395/128.0;

p11[8]=0.0;

p11[9]=-230945/256.0;

p11[10]=0.0;

p11[11]=88179/256.0;





int k;

vector<double>hx;

k=0;for(int i=0;i<k+1;i++)	hx.push_back(p0[i]);

k=1;for(int i=0;i<k+1;i++)	hx.push_back(p1[i]);

k=2;for(int i=0;i<k+1;i++)	hx.push_back(p2[i]);

k=3;for(int i=0;i<k+1;i++)	hx.push_back(p3[i]);

k=4;for(int i=0;i<k+1;i++)	hx.push_back(p4[i]);

k=5;for(int i=0;i<k+1;i++)	hx.push_back(p5[i]);

k=6;for(int i=0;i<k+1;i++)	hx.push_back(p6[i]);

k=7;for(int i=0;i<k+1;i++)	hx.push_back(p7[i]);

k=8;for(int i=0;i<k+1;i++)	hx.push_back(p8[i]);

k=9;for(int i=0;i<k+1;i++)	hx.push_back(p9[i]);

k=10;for(int i=0;i<k+1;i++)	hx.push_back(p10[i]);

k=11;for(int i=0;i<k+1;i++)	hx.push_back(p11[i]);

hx.resize(hx.size());



return hx;



}





    本章 9 章の説明へ

当 Page から他の page へ

風と翼 Windandwing は、c++の数値計算から風と翼の計算へ を目的とした数値計算を行っています。

第9章 数値積分(離散系) 等間隔、不等間隔データ(Newton-Cotes法)、級数展開

等間隔の離散データの数値積分(Newton-Cotes法)

不等間隔の離散データの数値積分(Newton-Cotes法)

不等間隔の離散データ時の Legendre 多項式による級数展開

Information

ナビゲーション

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　風と翼 Windandwing は、c++の数値計算から風と翼の計算へを目的とした数値計算を行っています。

第9章数値積分(離散系) 　等間隔、不等間隔データ(Newton-Cotes法)、級数展開