�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@���Ɨ� Windandwing �́Ac++�̐��l�v�Z���畗�Ɨ��̌v�Z�� ��ړI�Ƃ������l�v�Z���s���Ă��܂��B

��8�� ���l�ϕ�(�A���f�[�^): Newton-Cotes�ALegendre�AGauss-Chebyshev
�@�A�����ɁA���l�ϕ� Newton-Cotes �@�ALegendre �@�AGauss-Chebyshev �@�K�p���A��͒l�Ƃ̔�r�ŁA��@�̗D���r���s�����B������A��̓I�Ȑ��l�ϕ��v�Z 1 �Ɏ����B�v�Z���x�̗ǂ����́ALegendre �@�AGauss-Chebyshev �@�ANewton-Cotes�@�̏��ł���B
�@���l�ϕ��ɂ́A�ϕ��� [a.b] �Ԋu�ōs�����@�ƕs���Ԋu�Őϕ����s�����@������B
�@f(x) �̐ϕ��� [a.b] �Ԋu�Őϕ�������@�́ANewton-Cotes �@�ƌĂ�A��`���ASimpson1/3 ���A
Simpson3/8 ���ABoole ��������B�����́A�敪�_(���_)�̐����قȂ�B
�@�s���Ԋu�ɂ́ALegendre �@�� Gauss-Ckebyshev �@������BLegendre �@�́A���̎������ɔԊu�̋敪�_
(���_) xi �� f( x��) �ɈقȂ�d�W����݂��čs���B Gauss-Chebyshev �@�͂��̎������ɕ��_�͔Ԋu�ł���
���A f(xj ) �̏d�W���͓����ł���B
�@�Ȃ��ALegendre �@�́A�O�͂����l�v�Z 5 �������ɋL�ڂ��� Legendre ���������瓱��������邪�AGauss-
Chebyshev �@�͑O�͂� Chebyshev �������Ƃ͊W���Ȃ��B
�@�@�@
�@���̊O�A������̈�܂ł������v�Z���@������B�����ł͐G��Ȃ��B
�@�����̐��l�v�Z�@�ɂ��AChebyshev��������3���A12���A25���ɂ��āA���l�ϕ����s���D����r�����B
������A��̓I�Ȑ��l�ϕ��v�Z 1 �Ɏ����B
Newton-Cotes�@
�@Newton-Cotes �@�́A�ϕ���̋�ԂԊu�ɕ����āA�ϕ�����B�����̗L���ȕ��@���ߎ��̎������ɕ����A
��ϕ����� f(x) �Ƃ���ƁA�ȉ��ƂȂ�B
�ϕ���� [x0,x1] �ŁA���̕��� ��=(x1-x0) �ł���B
�@�@1)1�����@�F��`��
�@�@�@h/2�E(f(x0)+f(x1))�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@ �@�@�@ �@�@�@�@ 8-N-1 ��
�@�@2)2�����@�FSimpson 1/3 ��
�@�@�@ h/2�E(f(x0)+4f(x0+h/2)+f(x1) )�E1/3 �@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@ 8-N-2 ��
�@�@3)3�����@�FSimpson 3/8 ��
�@�@�@h/3�E(f(x0)+3f(x0+h/3)+3f(x0+2h/3)+f(x1) )�E3/8�@�@�@�@�@�@�@�@�@�@�@�@ 8-N-3 ��
�@�@4)4�����@�FBoole ��
�@�@�@h/4�E(7f(x0)+32f(x0+h/4)+12f(x0+h/2)+32f(x0+3h/4)+7f(x1))�E2/45
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@ 8-N-4 ��
�@���̂悤�ɁA�敪�_�ł� f(x) �ɒ萔���|���āA���Z����Ɛϕ��l���Z�o�ł����@�ł���B
�@�܂��A�s���Ԋu�̗��U�f�[�^�ɑ���ϕ����@�́A���͂����l�v�Z 7 �Ɏ����B
�Q�l�}���G�X�~���m�t�������w���� �T���@��ꕪ���@P.252
�@�@�@�@�@(110.�߂ɃV���v�\���̌����̐���������A���Ԋu�̏ꍇ�ɂ��ċL�q����Ă���B)
Legendre�@
1�A�v�Z�̊T�v�@�@���̕��@�́A�ϕ��� [a,b] �� [-1,1] �ɕϊ����ALegendre �������̉��_ xk �Ƃ��āA���_ xk �ɑΉ���
�@���d�W����p����B
�@�@�@
�@�@�@�@�@�@
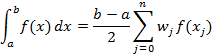 �@�@�@�@�@�@�@�@�@ �@ �@ �@�@�@�@�@�@�@�@ 8-L-1 ��
�@�@�@�@�@�@�@�@�@ �@ �@ �@�@�@�@�@�@�@�@ 8-L-1 �� �@��L�� f(xj ) �̎Z�o�́A[-1,1] �ł� Legendre ������ Pn �̉� xk �ɗ̈� [a,b]����ϊ����� xj �� �� f(xj )
�@�ɑ�����A�s���B
�@ �@�@�@�@�@
�@�@�d�W�� w�� �� Legendre �������̉��ł��镪�_ xk �ɑΉ������l�ŁA���̎�����Z�o�����B���̒l�́A
�@�ϕ��� [a,b] �ɂ͊W���Ȃ��Axk �݂̂ɂ��B�]���ALegendre ������ Pn �̎������ɁA�������Ɠ����d�W
�@���������ɂȂ�B��U�A���ꂼ��̒l��m��A��ϕ��Ώۂ̊��ɊW�Ȃ��g�p�ł���B
�@�@�@�@�@�@
�@���邢�́A
�@�@�@�@�@�@
�@�@��L�̌v�Z���\�ƂȂ闝�_�I�ȍl���́A������web��ł����J����Ă���B���̊T�v�́A��(x) �� 2n-1 ��
�@�̑������Ƃ��APn �� Qn-1 �̐ςƏ�]�� R(x) �œW�J�ł���Ƃ���BPn(x) �̑S�Ẳ��Ő��藧���O�����W
�@�F�������ŁA��(x) ���ߎ��ł���̂ŁA���𐫂����� Legendre �������̉����番�_�Əd�W���鎖���o
�@����Ƃ����l���ł���BLegendre �������̒��𐫂͑O�͂����l�v�Z 5 �������Ɏ����B
�@�@�����̍l���Ń��O�����W�F���������� Legendre �������ւ̓]���Ƃ��̋t�������_�ł���B
2�A���_ xk �Əd�W�� wj �Z�o
�@�@���_ xk ��Legendre�������̉��ł���BLegendre ������ Pn �̋�̓I�Ȏ��́A���l�v�Z 5 ��������
�@34 ���܂Ŏ����Ă���B���Q�Ƃ��Ă������������B
�@�@
�@�@6���܂ł�Pn�́A�ȉ��ł���B
�@�@�@�@
�@�@�@�@2��
�@�@�@�@�@ �@
�@�@�@�@3��
�@�@�@�@�@�@
�@�@�@�@4��
�@�@�@�@�@�@
�@�@�@�@5��
�@�@�@�@�@�@
�@�@�@�@6��
�@�@�@�@�@ �@
�@�@��L�̎��̉��A���Ȃ킿���_�͉��\�̒ʂ�ł���B
�@�@�@�@�@ �@�@�@�@�@
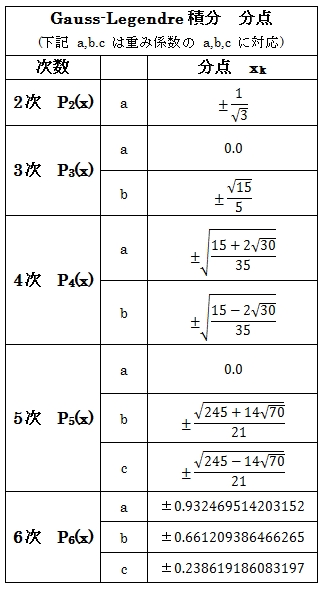
�@�@�Ȃ��A��L��6�� P6 �͉��Ɉȉ������B
�@�@�@�@�@�@�@
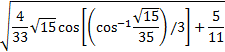 �@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@8-L-10 ��
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@8-L-10 ���@�@�@�@�������A���p�I�łȂ��̂ŁA0.932469514203152�Ƃ����B
�@�@��q�̉��ɑΉ������d�W�������߂�ɂ́A�������K�v�ƂȂ�B��̓I�ɂ́A4���̏ꍇ�AP4 �̓����͎�
�@���ƂȂ�B
�@�@�@�@�@�@
�@�@�]���A8-L-3 ���́A�ȉ��̎��Ŏ������B
�@�@ �@�@�@�@
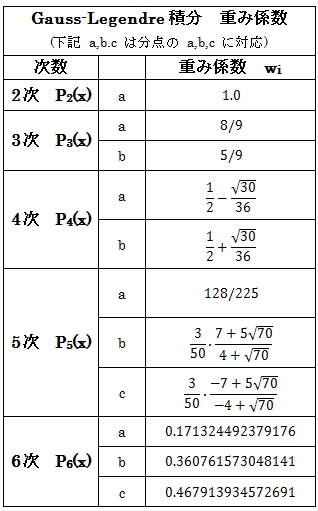
�@�@4���̉��@xk=sqrt((15.+2*sqrt(30.))/35) �̎��́A�ȉ��ŎZ�o�ł���B
�@�@�@�@ �@�@
 �@�@ �@�@8-L-13 ��
�@�@ �@�@8-L-13 ���@�@��L�̂悤�ɂ��ē��� Pn ��6���܂ł̏d�W���������B
�@�@�@�@�@�@�@
�@ �@�܂��A[-1,1] �̐ϕ���̒������̕��_�̏d�W���͑��̕��_�̏ꍇ���傫���BNewton-Cotes�@�̏ꍇ��
�@�@�����ł���B
�@ �@�Ȃ��Axk �̗̈� [a,b] �ւ̕ϊ��l xj �̋�̓I�ȎZ�o�ɂ��ẮA��̓I�Ȑ��l�ϕ��v�Z1�Ɏ����B
Gauss-Chebyshev�@
1�A�v�Z�̊T�v�@�@�@����Chebyshev�@�́A�Ԋu�̕��_ xj �������A�d�W�� wj �����̎����œ���ł�����������B
�@�@f(xj) �� wj �̐ς̉����Ȃ����_�����B�܂��AChebyshev������(�O�͂ɋL��)�Ƃ͊W���Ȃ��B
�@�@���̌v�Z�̍l���́A
�@�@�Ef(x) �� [-1,1] �Őϕ������l���Af(x1),f(x2),... f(xn) �̘a�ɒ萔 k ���|�����l�ɂقړ������Ɖ��肷��B
�@�@�@�@
�@�@�@�@�@�@ �@
�@�@�@�@�@
�@�@�@�@�������A�㎮�Ł@R(x) �͎c�]�Ƃ���B
�@�@�E���� f(x) �� (n+1) �K�܂œ��������Ƃ��A�}�N���[�����W�J���s���B
�@�@�@�@�@�@ �@
�@�@�E8-C-1���̉E�ӂ̃��̕��������߂�B�㎮�̍��� f(x) �� x �� x1,x2,.. xn ��������ƈȉ��ƂȂ�B
�@�@�@�@�@�@ �@
�@�@�@�@�@�@ �@
�@�@�@�@�@�@�@�E�E�E
�@�@�@�@�@�@�@
�@�@�E�㎮�̘a f(x1)+f(x2)+�E�E�E+f(xn) �� k ���|����ƁA8-C-1 ���̉E�ӂ����܂�A �ȉ��̎��ƂȂ�B
�@�@�@�@�@�@�@
�@�@�@�@�@�@�@�@�@�@
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@ �@�@�@�@�@�@�@�@�@
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@ �@�@ �@8-C-6��
�@�@�E8-C-1 ���̍��ӂ� [-1,1] �ł� f(x) �̐ϕ������߂�B 8-C-2 ���̃}�N���[�����W�J����ϕ�����B
�@�@�@�@�@�@�@
�@�@�@�@�@�@�@�@�@�@�@�@�@
�@�@�@���ɒ萔�ł��� f(0),f'(0) ����ϕ��L���̑O�ɏo����
�@�@�@�@�@�@�@�@�@�@�@�@
�@�@�@�@�@�@�@�@�@�@�@�@�@
�@�@�@x �̊���̐ϕ��́Ax �̋������ɂȂ�A�ϕ��悪 [-1,1] �̂� (-1)2p - (1)2p = 0 �ƂȂ�A�ȉ��ƂȂ�B
�@�@�@�@�@�@�@
�@�@�@�@�@�@�@
�@�@�@�@�@�@�@
�@�@�@�܂��Ax�̋������̐ϕ��́A�ȉ��ƂȂ�B
�@�@�@�@�@�@�@
�@�@�@���ʁA8-C-1 ���� f(x) �� [-1,1] ��̐ϕ��͈ȉ��ƂȂ�B
�@�@�@�@�@�@�@
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@
2�AChebyshev�@�̐��l�ϕ��̏����Z�o
�@�@�E8-C-1 ���̗��ӁA8-C-6 ����8-C-11���̔�r�ɂ��A���̎��i�����j�鎖���o����B
�@�@�@�@
�@�@�@1�j
�@�@�@2) ����� xj �ɂ���
�@�@�@�@�@�@�@
�@�@�@3)�������� xj �ɂ���
�@�@�@�@�@�@�@
3�AChebyshev�@�̏d�W���ƕ��_�̎Z�o���@
�@�@��L 3 ���������� xj �����߂鎖���o����Af(x) �̐ϕ����A�����̂悤�ɁA�ߎ��ł��鎖�ɂȂ�B
�@�@�@ �@�@�@�@
�@�@���Ȃ킿�Axj ���܂W���������Ƃ���
�@�@�@2 ���� ( 2���_ )�͈ȉ��̎��ƂȂ�B
�@�@�@�@�@�@�@
�@�@�@�@�@�@�@
�@�@�@3����(3���_)�͈ȉ��ƂȂ�B
�@�@�@�@�@�@�@
�@�@�@�@�@�@�@
�@�@�@n ����(n���_)�͈ȉ��ŁA���ꂼ��̌W���� xj ���܂�ł��鎮�ƂȂ�B
�@ �@�@�@�@�@�@
�@�@�@�@�@�@�@
�@�@�@�㎮�̂��ꂼ��̌W���̒l��8-C-12 ���A8-C-13 ���A8-C-14 �����狁�߂���@�����X�߂Ɏ����B
4�AChebyshev�@�̏d�W���ƕ��_
�@�@�E�d�W���F
�@�@�@�@�@�@�@
�@�@�E2��(2���_)�F 2���_�鎮
�@�@�@�@�@�@�@
�@�@�E3��(3���_)�F 3���_�鎮
�@�@�@�@�@�@�@
�@�@�E4��(4���_)�F 4���_�鎮
�@�@�@�@�@�@�@
�@�@�E5��(5���_) �F 5���_�鎮
�@�@�@�@�@�@�@
�@�@�E6��(6���_)�F6���_�鎮
�@�@�@�@�@�@�@
�@�@��L�̂܂Ƃ߂Ƃ��āAChebyshev�ϕ��̏d�W���ƕ��_�����\�Ɏ����B
�@�@�@�@�@�@�@

�@�@�@�Ȃ��AG6(x)�̉��ɁA�ȉ������A���p�I�łȂ��̂ŁA0.866246818107821�Ƃ����B
�@�@�@�@�@�@�@�@
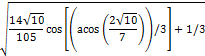 �@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@8-C-27��
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@8-C-27��5�A���_�����߂鎮�̎Z�o�i 8-C-22 ������ 8-C-26 �� �̍���)
�@�@�E2����( 8-C-22 �� �̎Z�o����)
�@�@�@�@x �� 2 ���ł̕��_�����߂鎮�́A8-C-20 ���� 2 ���`���ŁA�ȉ��ł���B
�@�@�@�@�@�@�@
�@�@�@�@�㎮��W�J����ƁA
�@�@�@�@�@�@�@
�@�@�@�@2�����ł́An=2�ł���̂ŁA�d�W����
�@�@�@�@�@�@�@k=2/2=1�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@8-C-30��
�@�@�@�@�� 1 ���̌W���́A�ȉ��ƂȂ�B
�@�@�@�@�@�@�@(x1+x2)=0 �@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@ �@�@�@�@�@�@�@�@�@�@ 8-C-31��
�@�@�@�@�@�@�@�@�@�@�@�@�@�@��8-C-13 �����@(x1+x2)=0 �@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@8-C-32��
�@�@�@�@�� 2 ���̌W���́A�ȉ��ƂȂ�B
�@�@�@�@�@�@�@2�Ex1�Ex2 = (x1+x2)2- (x12+x22) = 0 - 2/3 = - 2/3 �@�@�@�@�@�@�@�@ �@�@�@ 8-C-33��
�@�@�@�@�@�@�@�@�@�@�@�@�@�@��8-C-14�����@ x12+x22 = 2/(2*1+1)�@�@�@�@�@�@�@�@�@�@�@8-C-34��
�@�@�@�@�]���A
�@�@�@�@�@�@�@
�@�@�E3����( 8-C-23 ���̎Z�o����)
�@�@�@�@x �� 3 ���ł̕��_�����߂鎮�́A8-C-20 ���� 3 ���`���ŁA�ȉ��ł���B
�@�@�@�@�@�@�@
�@�@�@�@�㎮��W�J����ƁA
�@�@�@�@�@�@�@
�@�@�@�@3�����ł́An=3 �ł���̂ŁA�d�W����
�@�@�@�@�@�@�@k=2/3�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@ �@ 8-C-37��
�@�@�@�@�� 1 ���̌W���́A
�@�@�@�@�@�@�@(x1+x2+x3)=0 �@ �@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@ �@�@8-C-38��
�@�@�@�@�@�@�@�@�@�@�@�@�@�@��8-C-13�����@(x1+x2+x3)=0
�@�@�@�@�� 3 ���̌W���́A
�@�@�@�@�@�@�@2�E(x1�Ex2+x2�Ex3+x3�Ex1)= �ix1+x2+x3)2- �ix12+x22+x32) = 0 -1 = -1
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@ �@�@ 8-C-39��
�@�@�@�@�� 4 ���̌W���́A
�@�@�@�@�@�@�@-3�Ex1�Ex2�E��3=
�@�@�@�@�@�@�@�@�@�@�@�@(x1+x2+x3)3- (x13+x23+x33) - 3 (x1+x2+x3)�E(x1�Ex2+x2�Ex3+x3�Ex1)
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@ =0 - 0- 3�E0�E(-1/2)= 0 �@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@ �@8-C-40��
�@�@�@�@�@�@�@�@�@�@�@�@�@�@��8-C-13�����@x13+x23+x33=0�@�@ �@�@�@�@�@ �@�@�@�@�@�@ 8-C-41��
�@�@�@�@�]���A
�@�@�@�@�@�@�@
�@�@�E4����( 8-C-24 ���̎Z�o����)
�@�@�@�@x �� 4 ���ł̕��_�����߂鎮�́A8-C-20 ���� 4 ���`���ŁA�ȉ��ł���B
�@�@�@�@�@�@�@
�@�@�@�@�㎮��W�J�����
�@�@�@�@�@�@�@
�@�@�@�@�@�@�@�@�@�@�@�@
�@�@�@�@ 4�����ł́An=4 �ł���̂ŁA�d�W����
�@�@�@�@�@�@�@k=1/2
�@�@�@�@�� 2 ���̌W���́A
�@�@�@�@�@�@�@(x1+x2+x3+x4)=0 �@�@(��8-C-13����� 0 )�@�@�@�@�@�@�@�@�@�@�@ �@�@�@�@�@ 8-C-44��
�@�@�@�@�� 3 ���̌W���́A
�@�@�@�@�@�@�@2�E'(x1�Ex2+x2�Ex3+x3�Ex4+x4�Ex1)=(x1+x2+x3+x4)2- �ix12+x22+x32+x42)
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@ = 0 - 4/3 = - 4/3 �@�@�@�@�@�@�@ �@�@ 8-C-45��
�@�@�@�@�@�@�@�@�@�@�@�@�@�@��8-C-14�����@x12+x22+x32+x42 = 2�E2/1/(2*1+1) = 4/3
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@ �@�@�@�@�@�@�@ 8-C-46��
�@�@�@�@�� 4 ���̌W���́A
�@�@�@�@�@�@�@-3(x1�Ex2�E��3+x2�Ex3�E��4+x3�Ex4�E��1+x4�Ex1�E��2)
�@�@�@�@�@�@�@�@=�ix1+x2+x3+x4)3
�@�@�@�@�@�@�@�@�@�@- �ix13+x23+x33+x43)
�@�@�@�@�@�@�@�@�@�@-3 �ix1+x2+x3+x4)�E(x1�Ex2+x2�Ex3+x3�Ex4+x4�Ex1+x4�Ex2+x1�Ex3)
�@�@�@�@�@�@�@�@ = 0
�@�@�@�@�@�@�@�@�@ - 0
�@�@�@�@�@�@�@�@�@- 0
�@�@�@�@�@�@�@�@ =0 �@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@ 8-C-47 ��
�@�@�@�@�@�@�@�@�@�@�@�@�@�@��8-C-13 �����@x1+x2+x3+x4=0
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@x13+x23+x33+x43=0
�@�@�@�@�� 5 ���̌W���́A
�@�@�@�@�@�@�@�@-12�Ex1�Ex2�E��3�E��4
�@�@�@�@�@�@�@�@�@=�ix1+x2+x3+x4)4
�@�@�@�@�@�@�@�@�@�@ + 3�ix14+x24+x34+x44)
�@�@�@�@�@�@�@�@�@�@�@- 6(x1�Ex2+x2�Ex3+x3�Ex4+x4�Ex1+x4�Ex2+x1�Ex3)2
�@�@�@�@�@�@�@�@�@�@�@- 4(x13+x23+x33+x43)�ix1+x2+x3+x4)
�@�@�@�@ �@�@�@�@ = 0
�@�@�@�@�@�@�@�@�@�@+3�E(4/5)
�@�@�@�@�@�@�@�@�@�@-6�E(-2/3)�E(-2/3)
�@�@�@�@�@�@�@�@�@�@-4�E0
�@�@�@�@�@�@�@�@�@=-4/15
�@�@�@�@�@�@�@�@�@�@�@�@��8-C-14�����@ x14+x24+x34+x44=2�E2/1/(2*2+1)=4/5
�@�@�@�@�@�@�@�@�@�@�@�@�@�܂��A��3���̌v�Z���ʂ��㎮�̎O�Ԗڂ̍��ɑ������B
�@�@�@�@�@�@�@�@�@���@x1�Ex2�E��3�E��4=1/45
�@�@�@�@�]���A
�@�@�@�@�@�@�@
�@�@�E5����( 8-C-25 ���̎Z�o����)
�@�@�@�@���̎��̊e���̌W���̎Z�o�ߒ��ƒl�́A�����O�͎��������A���͎����Ȃ��B����Ɏ����B
�@�@�@�@���݁A�����̓\��t�������̂܂ɂ��o���Ȃ��Ȃ��Ă���̂ŁA�������@2014/2/7
�@�@�E6����( 8-C-26 ���̎Z�o����)
�@�@�@�@�v�Z���s��
6�A���̑�
�@�@�ϕ��� [a,b] �ւ� [-1,1] ��̕��_�̕ϊ��͋�̓I�Ȑ��l�ϕ��v�Z�̌��Ŏ����B
�Q�l�}���F���l�v�Z�n���h�u�b�N
�@�@�@�@�@�V���l�v�Z�@�@�����͒��A�T�C�G���X�Џo��
��̓I�Ȑ��l�ϕ��v�Z1�i��Ώ� Chebyshev ������)
1�A���l�ϕ��v�Z (�R�[�h1)�@���l�ϕ��̎�@�ɂ́A�O�q�̂悤�ɁA�e�킠��B�ǂ̕��@����ʓI�Ȋ��ɑ��Č��ʓI�ł��邩��m�邽�߂ɁA��̓I�Ɍv�Z���s�����B
�@
�@�A�����ł��� Chebyshev�������ɁA���l�ϕ� Newton-Cotes �@�ALegendre �@�AGauss-Chebyshev �@�K�p���A��͒l�Ƃ̔�r�ŁA��@�̗D���r���s���B
�@���_�������ƁA�v�Z���x�̗ǂ����́ALegendre �@�AGauss-Chebyshev �@�ANewton-Cotes�@�̏��ł���B�@
2�A���l�ϕ��v�Z�̐���
�@1) [-1,1] ���̓_����ϕ���ma,b] �ւ̓_�ւ̕ϊ�
�@�@ ���̐ϕ���̕ϊ��́A8-L-2 ���� xj = (b+a)/2 + (b-a)xk/2 ��p���čs�����ɂȂ�B
�@�@�@b-a = h �̎��Ab = a+h �ŁA(b+a)/2 = (h+2a)2 = a+h/2 �ƂȂ�B�ϕ��̉����_ a �� ��/2 ���v���X��
�@�@��悢���ɂȂ�B�]���A�ȉ��ƂȂ�B
�@�@�@�@�@�@�@
�@2)���l�ϕ��̑Ώ�
�@�@�E���l�ϕ��̎�@
�@�@�@�@Gauss-Legendre�@ �F2�A3�A4�A5�A6�@���_�i�����j
�@�@�@�@Chebyshev�@�@�@�@�F2�A3�A4�A5�A6�@���_�i�����j
�@�@�@�@Newton-Cotes�@ �@�F��`���ASimpson 1/3 ���ASimpson 3/8 ���ABoole��
�@�@�E��v�Z�� �@Chebyshev������
�@�@�@�@(1) 3 �����A�@�ϕ��� [2,6]�A�@��� 1232
�@�@�@�@�@�@�s3(x)=4x3-3x
�@�@�@�@�@
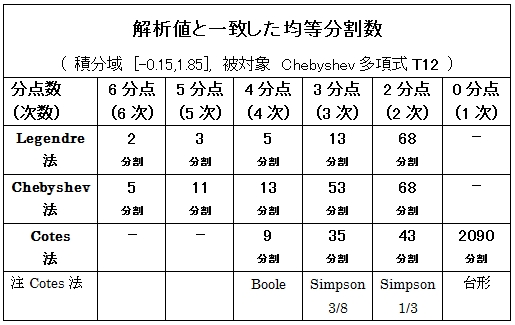
�@�@�@�@(2) 12 �����A �ϕ��� [-0.15,1.85]�A�@ ��� 143632.865175008
�@�@�@�@�@�@T12(x)=2048x12-6144x10+6912x8-3584x6+840x4-72x2+1
�@�@�@�@(3) 25 �����A�@�ϕ��� [-0.95,1.05]�A ��� 14.6430725603351
�@�@�@�@�@�@T25(x)=16777216x25-104857600x23+288358400x21-458752000x19+466944000x17-
�@�@�@�@�@�@�@�@�@�@-317521920x15+146227200x13-45260800x11+9152000x9-1144000x7+80080x5-
�@�@�@�@�@�@�@�@�@�@-2600x3+25x
3�A���l�ϕ��̎�@�̕]��
�@�@��L (1)�A(2)�A(3)�̐ϕ��� [a,b] ���ϓ��ɕ������A���̋敪�̒��ŕ��_�Əd�W�����g�p���A���Ȃ�����
�@�@���ʼn�͒l�ɓ��B���������]�������B
�@�@�������̏��Ȃ����@ (���x�����l���镪�����̏��Ȃ����Ő��肵��)
�@�@�@�@
�@�@�@�@����1�AGauss-Legendre 6���_
�@�@�@�@����2�AGauss-Legendre 5���_
�@�@�@�@����3�AChebyshev 6���_
�@�@�@�@����4�AGauss-Legendre 4���_
�@�@�@�@����5�ABoole��
�@�@�@�@����6�AChebyshev 5���_
�@�@�@�@����7�AChebyshev 4���_
�@�@�@�@����8�AGauss-Legendre 3���_
�@�@�@�@����9�ASimpson 3/8��
�@�@�@�@����10�ASimpson 1/3��
�@�@�@�@����11�AChebyshev 3���_
�@�@�@�@����12�AChebyshev 2���_�AGauss-Legendre 2���_
�@�@�@�@����14�A��`��
�@�@�@�@�Ȃ��AChebyshev��2���_�� Gauss-Legengre��2���_�́A�����d�݁A���_�ł���̂ŁA�������ʂ�B
4�A�v�Z���ʂ̈ꗗ
�@�@�@1�jChebyshev�������@T3��
�@�@�@�@�@�@�@�@

�@�@�@2)Chebyshev�������@T12��
�@�@�@�@�@�@�@�@
�@�@�@3)Chebyshev�������@T25��
�@�@�@�@�@�@�@�@

5�A�g�p����STL
�@�@ vector<double>fx�Ainner_product()
��̓I�Ȑ��l�v�Z2�i�\��)
Information
�@�@�@�@�@
- 2012�N
- ���̏͂̓�������
2012�N1���@2011�N�� ���l�ϕ��Ɛϕ��������̏͂̈ꕔ�� �@ - 2012&13�N
- ���̏͂̕ύX�lj�����
10)�^���[�A�䉑�̉摜��lj� 2013/9/28
9)�h�Ђ���2���̏H�ɍ��ւ��@2013/9/28
8)�g�}�g�A�ԁASkytree�A��q��A�s���̉摜�̒lj��@2013/9/27
7)�摜�̒lj��@2013/05/12
6)Chebyshev�ϕ���4�����̑�5���W���̎Z�o�������̋L�ځ@2012/11/20
5)Chebyshev�ϕ���4�����̑�4���W���̎Z�o�������̋L�ځ@2012/10/26
4)��̓I�Ȑ��l�ϕ��v�Z1�̋L�ځ@2012/3/25
3)Gauss-Chebyahev�@�̋L�ځ@2012/3/23
2)Legendre�@�̋L�ځ@2012/3/22
1)Newton-Cotes�@�̋L�ځ@2012/3/21
























































