逆ラプラス・移動則・Bodeplot

第5章 逆ラプラス変換、移動則、Bode Plot

逆ラプラス変換である高速ラプラス変換(FILT)に、c++ を適用した。FILTの持つ失速・脱調の要因を検討し、対策を施し、失速・脱調の発生をなくした。これにより、実用的な計算になった。
更に、逆ラプラス変換の計算では、移動則も必要とされるので、FILTで移動則の確認を行った。

また、この逆ラプラス(FILT)を Feedback回路(次章の第6章)、Bode Plot に適用した。

次章6章に、高速ラプラス変換は、Euler変換を使用しているので、Euler変換を 62次まで記載する。62次までの記載は、順次、行っていく。ホームページの footer に記載すると、スペースが広くとれるようになったために。
なお、Euler変換は、二項係数が源になっているので、二項係数も同様に、62次まで順次記載する。

１、逆ラプラス変換

1、逆ラプラス変換(コード1)　FILTによる計算　(安定系)
　計算の動機
　"Cによる科学技術計算"小池慎一著に記載の計算をc++/STLにより逆ラプラス変換の計算を行った。しかし、計算
　結果が1.0であるべきところが0.8になった。このために、小池氏の逆ラプラス変換の参照本の"BASICによる高速
　ラプラス変換"細野敏夫著(共立出版、1984)を調査した。この本の計算は、(1)付録Bの複素関数論による部分分数
　展開と(2)オイラー変換を基に計算が行われている。

　コードに示すように、ラプラスの逆変換が容易に精度高く計算出来た。今も、この本が学会の論文で引用される
　所以が判った。この本を細野本とよぶ。

　以下、虚数(√-1)を i、, j 、#i で示す。ｊは、電気では、電流を i で示す場合があり、これとの混乱を避けるため
　に用いる時がある。#iは、繰り返しの i と区別するため。

　1)"BASICによる高速ラプラス変換"の付録B"FILTの理論式の誘導"の説明
　　(1)付録Bの概要
　　　Bromwich積分B.1式の指数関数を近似式で置き換える事で、FILTは成立している。

　　　　　　　　　　　　　　　　　　　　　　　　（B.1)式

　　　この都合のよい近似式(B.2)式は、極を持つ、分母にゼロ点を持つ式である。

　　　　　　　　　　　　　　　　　　　　　　　　　　（B.2)式

　　　注、細野本の(B.3)式は、a>>Re(s)の時に、(B.2)式がのよい近似である事を示す式。

　　　(B.2)式を部分分数に展開すると、(B.4)式になり、FILTの理論式の導出根拠である。

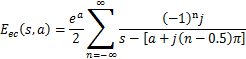　　　　　　　　　　　　　　　　　　　(B.4)式

　　　(2)付録Bの(B.4)式の因数分解の説明
　　　　(B.2)式から(B.4)式の因数分解については、Homepageにて逆ラプラスを記述されている荒畑氏(Tokyo
　　　　-pax 南中野パソコン教室　http://www.tokyo-pax.co.jp/tokyopax1
　　　　の数式処理ソフトDERIVE(デライブ) de ドライブ))にご教授いただいた。この方は、数学セミナーの
　　　　通巻0号にも執筆されている。このご教授いただいた内容を公開し、多くの人の疑問に役立てる。
　　　　　
　　　　ご教授いただいた内容を下記に示す。しかし、ご教授内容をそのままでは、失礼にあたるので、(3)にこの
　　　　考えの補強を示す。

　　　　ご教授内容
　　　　　まず、(B.2)式内の cosh(a-s) のゼロ点は、s=a+(2n-1)・π・#i/2 となる。(π：パイ) 　これらは、
　　　　すべて、単根となる。ここで、n=-∞ ～ +∞ まで動く。普通は、s＝a＋(2n+1)π×#i/2 と書くが、細
　　　　野本に合わせて、このように書く。なお、aは、正の実数、#iは、虚数単位である。

　　　　　(B.2)式の 1/cosh(a-s) の部分は、上記のゼロ点を s(k) と表すと、1/Π(s-s(k))、ここで、Πは、乗積
　　　　記号、k＝－∞～＋∞ である。この式は、Σb(k)/(s－s(k))のように部分分数に展開される。

　　　　　このb(k)は、初等的にも、以下を繰り返して、適用する事により求める事はできる。

　　　　1/((s-a1)(s-a2))=(1/(a1-a2))(1/(s-a1)-1/(s-a2))

　　　　　ただ、複素関数論的に、係数 b(k) は s=s(k) での留数そのものであるので、第50回目の留数の章にも記
　　　　載したように、

　　　　b(k)=lim(s → s(k)) (s-s(k))/cosh(a-s) = (-1)^k・#i と求まる。

　　　　従い、(B.2)式は、

　　　　exp(a)/2・Σ((-1)^n・#i/(s-(a+(2n-1)π・#i /2))=exp(a)/2・Σ((-1)^n・#i/(s-(a+(n-0.5)π・#i))

　　　　となる。結果、(B.4)式と一致する。　注、π はパイ。

　　　　補足；第50回目の留数の説明は、南中野パソコン教室の数式処理ソフトDERIVE(デライブ)
　　　　　　　de ドライブに記載されている。

　　 (3)付録Bに関する教授内容の補強
　　　　a)部分分数分解の初等的な解法
　　　　　以下の有限個の乗積P(z)があった時、文献(1)のp130のように

　　　　　　　　　　　　　(1)式

　　　　　は、(2)式のように部分分数に分解できる。

　　　　　　　　　　　　　(2)式

　　　　　(2)式の分子の係数b₁、b₂、... .b_n、は　(2)式の両辺に(1)式を掛けると(3)式となる。

　　　　　　　　　　　　　　　　　　　　

　　　　　　　　　　　　　　　　　　　　　　　　　(3)式

　　　　　更に、(3)式のzにa₁を代入すると、係数b₂ 項以降は(a₁-a₁)を持つので、ゼロとなり、b₁ の係数のみの
　　　　　項が残り、以下となる。

　　　　　　

　　　　　従い、b₁ は以下の(4)式となる。

　　　　　　　　　　　　　　　　　　　　　　　　(4)式

　　　　　また、(3)式のzにa₂を代入すると、係数b₂ の項以外は(a₂-a₂)のためゼロとなる。

　　　　　　

　　　　　　　　　　　　　　　　　　　　　　　(5)式

　　　　　同様に、(3)式のzにa_nを代入すると、係数b_nの項以外はゼロとなる。

　　　　　　

　　　　　従い、係数b_n は以下の(6)式となる。

　　　　　　　　　　　　　　　　　　　　　　　(6)式

　　　　　この場合、係数b_n の分母は、有限のn-1個で構成されているので計算できない訳ではない。し
　　　　　かしながら、無限の個数の場合は、初等的な方法では計算できない。このために、複素関数論
　　　　　の留数定理を用いて算出する事が必要になる。

　　　　b)留数定理による係数bの算出　
　　　　　・cosh(πz)の無限乗積の表現は、ウィキペディア双曲線に記載のように以下となる。

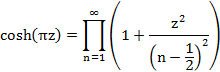　　　　　　　　　　　　　　　　　　　　　　(7)式

　　　　　　上記の(7)式でｚを(s-a)/πとして、cosh(s-a)のゼロ点を算出すると、以下となる。

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　(8)式

　　　　　　この時に、虚数 i の前に±があるので、(7)式のnは-∞から＋∞までの値となる。

　　　　　　・1/cosh(a-s)の部分分数展開
　　　　　　　b(k)＝lim（s→s(k))（s－s(k)）／cosh（a-s）＝ (-1)^k×#i についても、以下のよう
　　　　　　　に荒畑氏にまたご教授いただいたので、公開する。

　　　　　　　1/cos(z)を部分分数に展開する問題を考える。　ここで、zは、複素数とする。上記の
　　　　　　　cos(z)のゼロ点は、(2k-1)π/2、k＝－∞～∞。
　　　　　　　留数の定理より、

　　　　　　　lim（z->(2k-1)π/2）（z－(2k-1)π/2）/cos(z)＝(-1)^k

　　　　　　　従って、1/cos(z)＝Σ(-1)^k/（z－(2k-1)π/2）となる。
　　　　　　　一方、cos（#i*s）＝cosh(s)であるので、上式で、zを#i*zと置き換えると、左辺は、
　　　　　　　1/cosh(z)となる。#iは虚数単位とする。右辺は、少し、計算すると、
　　　　　　　#i (-1)^k/(z-(2k-1)π#i/2) と変形できる。これは、1/cosh(z)の部分分数の係数が、
　　　　　　　#i (-1)^kであることを示している。

　　　　　　　荒畑氏に感謝感激。

　　　　　　　参考文献　(1) 鈴木紀明著　「数学基礎　複素関数」　培風館(2001)

　　(4)(B.1)式の指数関数部e^stの展開式(B,4)式の代入後の式
　　　　(B.1)式の指数関数部e^stに(B.4)式E_ec(s・t,a)を代入すると以下の式になる。

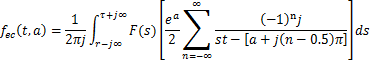　　　　　　　　　　　(B.6)a式

　　　　原文に補足する。ここで、極が s・t=a+j(n-0.5)πであるので、s(n)=[a+j(n-0.5)π]/t にの
　　　　みに、F(s) が存在する事になる。従い、

　　　　　　　(B.7)式

　　　　(B.7)式は、(B.6)aで、留数定理の採用で 1/2πｊが消えて、上式のΣ部の時間ｔを引き出した
　　　　ので、分母に t が存在する。しかし、原文の(-1)^nが(-1)^(n+1)の理由は判らない。誤植だ
　　　　ろう。

　　　　結論としてFILTの理論式は以下が最終の式となる。

　　　　　　

　　　　この最終式は、時間 t と伴に F(s) の s として、実数部の a/t と虚数部の (n-0.5)π/t を用い、
　　　　F(s) に代入し、F(s)　全体の虚数部を求め、それを集めて、exp(a)/t を掛けた時に、ある t
　　　　と a での逆ラプラス値を求める事を言っている。

　　　　また、(B.2)式の exp(a)/2cosh(a-s)がexp(s)/(1+exp(-2a+2s)) となるので、sのreal_part(
　　　　Re(s)=a/t)<<aならば、exp(-2a+2s)ゼロに近づき、exp(-a)、exp(-2a)で展開できるので、
　　　　aの値を大きくとれば近似誤差が小さくなる事を示す。

　　　　更に、(-1)^nの交代級数はeuler変換を行えば収束を速める事が出来る。

　　　　細野本の付録BのFILTについて、ここまで記載したのは、この本を読もうとすると、図書館にの
　　　　みあり、貸出期間も２週間であるために、後日、居住地が変わった時に読もうとしても困難であ
　　　　るので、記載した。小池慎一氏の記述は著作権にたいする配慮からかも知れないが、詳細な記述
　　　　がなかったので、補足した。

　　　　なお、Euler変換については、次章に示す

　　2) 具体的な計算(コード1)
　　　(1)計算の概略説明
　　　　・計算の実質部分を function 文 void reverse で行い、mainは繰返しの制御のみ。
　　　　・繰返しの回数は、時間軸であるx軸の長さに対応する。
　　　　・function文は、他のfunction文の呼び出しを無くし、単独の文にした。function文の第一ステ
　　　　　ップでは、始めの数項をそのまま計算し、第二ステップでは、euler変換の計算とした。この
　　　　　euler変換の詳細は、次章のeuler変換に示す。
　　　　　euler変換では、変換の次数を61次で、固定した。

　　　　・計算では、数値の小さい方からの加算となるようにし、精度低下を防止した。更に、小池本で
　　　　　の二項係数の算出計算とap[0]の掛け算と割り算を無くし、精度を上げるようにした。
　　　　・F(s)の分母分子をそれぞれ計算するようにし、判り易くした。
　　　　・c++には<complex>ヘッダーがあるので、imag_unit、real_unitを設け、 s の複素数化の
　　　　　計算を単純化した。

　　　　　従い、コードが始めから終わりまで一気通貫になり、単純になった。

　　　　・また、打ち切り誤差(trancation)の算出を試みた。

　　　(2)test計算　cosine（細野本、小池本ともに sin を対象にしていたので、変えてみた。）
　　　　 cosineとしての入力は、cosineのラプラス変換 s/(s^2+1) を計算するのではなく、

　　　　　　 (s^3 + 2s^2 + 3s + 0)/(s^4 + 2s^3 + 4s^2 + 2s + 3) 　( = s/(s^2 + 1) )

　　　　を与え、結果として cosine を求める入力である。
　　　　パラメータとして、Euler変換次数 p=61、FILT a=20、細野係数 k1=5、k2=0.5 を用いた。

　　　(3) 計算結果
　　　　　計算精度は、euler変換次数pとexp(a)のaを大きくすれば、精度が向上する事を確認した。

　　　　　細野係数と呼ぶべきk=k1+time・k2は、timeの値が増加すると、k値が大きくなり、第一ス
　　　　　テップの部分和の項数が増える。従い、この部分和の精度が上昇する事になり、結果として計
　　　　　算精度を上げている。test計算では、固定 k値でないために、計算の発散は無かった。

　　　　　FILT計算では発散の制御 (k=k1+time・k2)が重要である。

　　　(4)k値制御による発散制御の計算 (本章の 3項を参照ください。)
　　　　　　状況に応じ、k値を変える方法を採った。このk値を変える方法で、上記のcosineを対象に
　　　　　し、5000個のcosine波の計算を連続して、行ったが、失速・脱調はなかった。

このページの先頭へ

2、逆ラプラス変換（コード2）　FILTによる計算　（拡大系）
　1)時間の経過と伴に数値が無限に拡大していく拡大系
　　　これについても細野本は記述しているので、計算を行った。
　　　分母の解に実数 b が存在する場合で、変換するとexp(b*t)が存在する事になる。この場合には、
　　　FILTでは、上記の最後の式に、exp(a)/t に、exp(b*t)　を掛け、F[a/t+j(n-0.5)π/t] を
　　　F[b+a/t+j(n-0.5)π/t] と実数のbを付け加えればよいと説明している。この計算を行った。

　2)test計算
　　　exp(b*time)・sint(time) 　（細野本で取り上げられている試計算）
　　　分子； 1
　　　分母； s^2 - 2s + 2
　　　分母の解は　1± i であるので、 b=1.0 である。
　　　パラメータとして、Euler変換次数　p=61、FILTの a=5、細野係数 k1=20、k2=1.6、b=1.0
　　　上記のパラメータは、細野本の推奨値　p=6,a=6,k1=12,k2=0.4 と異なる。

　3) 計算結果
　　　計算結果は、time=78radian(1000回の繰返し)でもE-5の精度が得られた。
　　　拡大系でも FILT および当コードの有力さを確認した。

このページの先頭へ

3、逆ラプラス変換( コード3 )　FILTの失速あるいは脱調対策
　　FILT計算では、計算自体が収束しなくなる事、失速が生じる。これの対策として部分和の数を増
　　加させる方法が取られる。ここに記載するのは、部分和の増加の方法についての提案である。

　　FILTは、一方向に落下するように収束させる計算ではなく、単位円の壺の中の側面をらせん状にまわり
　　ながら収束させるというイメージ（交代級数の±を考慮しても、ある断面でみると±が現れる）の計算
　　であると想定できる。これが妨げられると失速/脱調するとし、部分和の数を増やす事を行う。

　1)FILT計算でEuler変換無しの場合の計算精度
　　　FILTは、交代級数の数項の和を算出し、以降の数項をEuler変換して、収束させる計算方法であ
　　　る。始めの数項とEuler変換との整合がよくない場合、失速散あるいは脱調が生じる。これは南中
　　　野パソコン教室のHomepage数式処理ソフト 数式処理ソフト DERIVE(デライブ) de ドライブ
　　　にも記載されている。この失速/脱調の要因に、上述のHomepageに記載されているようにEuler変換は、
　　　単調減少する時に有効であると言う前提が狂った時に起こる事を挙げる事が予想されるが。

　　　このために、Euler変換無しでFILT計算を実施した。

　　　計算対象　(s^3+2s^2+3s)/(s^4+2s^3+4s^2+2s^2+3)、 cosine.。
　　　計算条件　交代級数の項　50000（=ｋ)、 a=5、変換次数 p=0 (変換無し )、
　　　　　　　　連続計算回数10000で、刻みが0.07853・・・由、cosine数 125個

　　　計算結果　失速/脱調は無し。従い、Euler変換時の |a[n]| が単調減少でない場合に発散あるいは
　　　　　　　　脱調が生じると予想されるが。
　　　　　　　　しかし、計算精度は約0.6％ (FILT-cos(t)))/cos(t)×100 、悪い。更に約半時間の計算

　　　結論を言えば、FILTでは、Euler変換は省く事が出来ない事になる。そのために、計算過程で始めの
　　　単純和の項数(k値)を変えて行く事が前提になる。

　2)発散あるいは脱調の現象
　　　上記に示したように、単純和のみでは、失速/脱調はない。Euler変換との関係で生じる事になる。
　　　 Euler変換は、単なる収束の加速を行っているに過ぎない。それならば、単純和の部分にその予兆、
　　　引き金がある事になる。単純和とEuler変換の整合の問題ではないと考えられる。

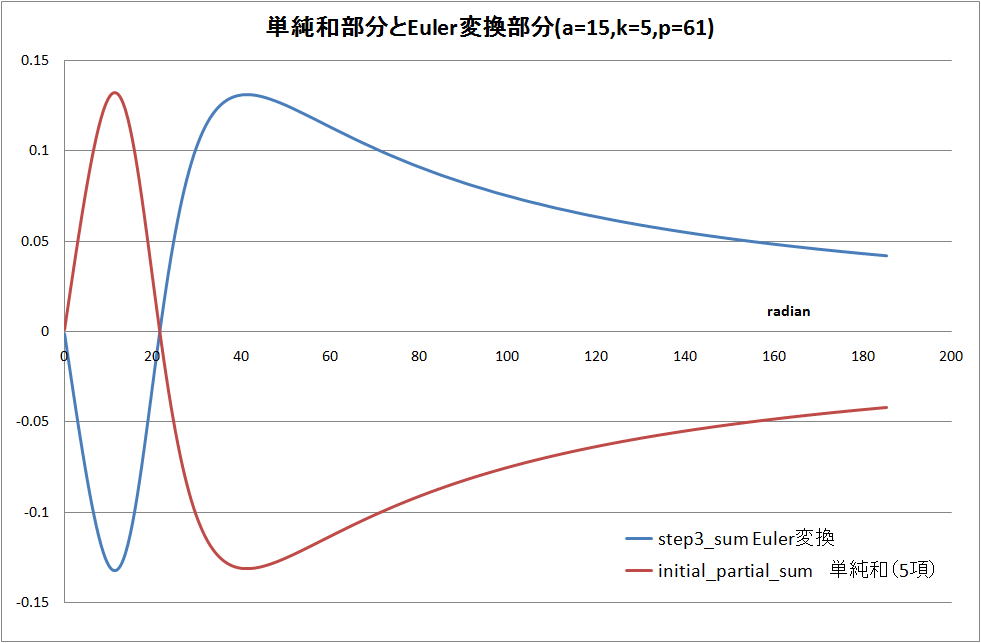
　　　上記と同じF(s)で(逆変換 cos(t) )のFILTの始めの単純和部分を 5 項(k=5)で計算（a=15,p=61)
　　　の結果を下図に示す。80 radianから失速/脱調し、遂にはFILT計算が出来なくなっている。

　　　　　

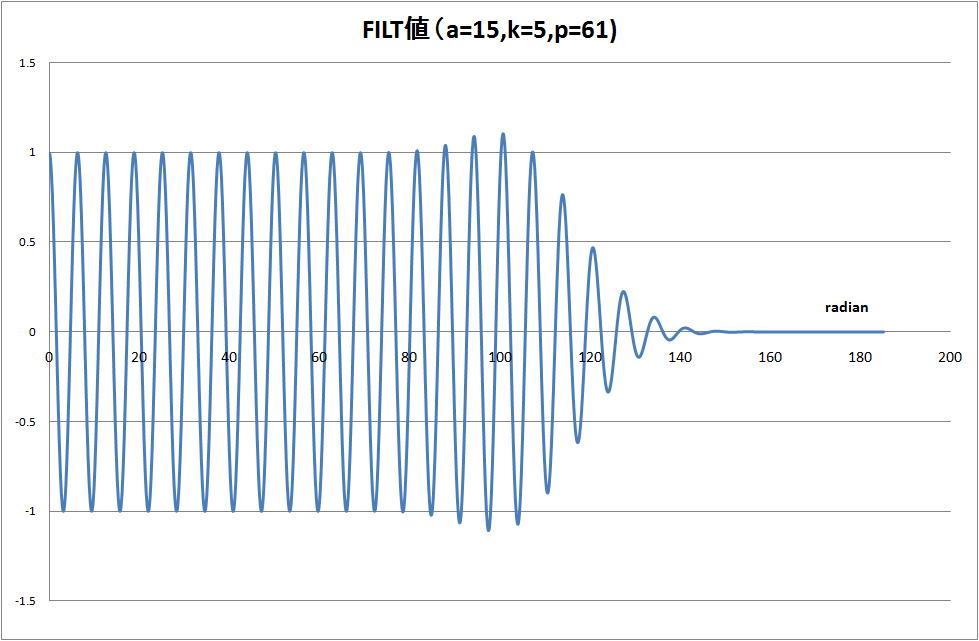
　　　これを、FILTの単純和部分(k=5)とEuler変換部分(次数p=61)に分けた計算結果を下図に示す。
　　　FILTの exp(a)/t を掛ける前の状態である。両者の僅かな差にexp(a)/t なる大きな数値を掛ける事
　　　で 1.0 程度の数値をFILTでは得ている。

　　　下図で、21.6radianで、5項の単純和とEuler変換の正負が変わってから再び正負が変わらずに、両
　　　者ともゼロに収束している。その結果、計算出来なくなっている。

　　　　　

　　　　上図の交点となった21.6radianの前後で何が起きているかと言えば、
　　　　　・21.52radianまでは、単純和の5項の各項の位相角が正負の状態が混在している。
　　　　　・21.60radian以降後では、単純和の5項の各項の位相角が全て正である。

　　　　具体的な位相角の計算結果を示すと、
　　　　　時間 21.52 radian、第1項　1.532、第2　0.644、第3　1.501、第4　1.264、第5　-1.570
　　　　　時間 21.60 radian、第1項　1.535、第2　0.638、第3　1.500、第4　1.254、第5　1.570

　　　　ここで言う位相角は、

　　　　　real_F(s)/imag_F(s)の角度 atan(real_F(s)/imag_F(s)) 　s=(a+j(k-0.5)π)/t

　　　　である。位相角で、F(s)の虚数側 imag_F(s) を分母にしたのは、atanでの計算の実行上の都合。

　　　　 kの一つの増加で、数式処理ソフト DERIVE(デライブ) de ドライブにも記述されているように、
　　　　発散/脱調までの時間が延びる。ｋが増加すると、21.6radianでは、上記には示していないが、
　　　　一つ増加した項、第6項の位相が負となるためである。

　　　　なお、刻みの精度を　3.14159265358979323846264338327950288/40.0　とすると、上図の
　　　　交差の時刻が約18radianと短くなり、各項の位相は上記の位相ではなくなるが、最後には各項の
　　　　位相は同位相となり、遂には、脱調/失速する。

　　　　各項間に位相の変化がないと発散/失速するという考えは妥当と考える。

　3)FILTの発散、失速・脱調防止方法
　　　　FILT計算で発散、脱調防止方法として、k値を単純和の各項の位相が全て正になる度に増加させる
　　　　と、時間 t の経過と伴にk値が極めて大きくなる可能性がある。発散、脱調に至るまでは、時間的には
　　　　余裕がある事が上図からも読み取れる。これを考慮して、各時間毎に、仮に単純和を数項増加(k値
　　　　増加)をさせた時にその中に負位相があれば、増加させない。無ければ増加させる方法を採った。

　　　　また、FILT計算の発散、脱調の引き金が単純和の各項の位相にあるので、Euler変換の次数が
　　　　高くても問題を生じないので、常時、次数が p=61でも良い事になる。

　　　　この考え（k値増加と高次のｐ）での単純和部分とEuler変換部分の計算結果を下図にに示す。

　　　　　

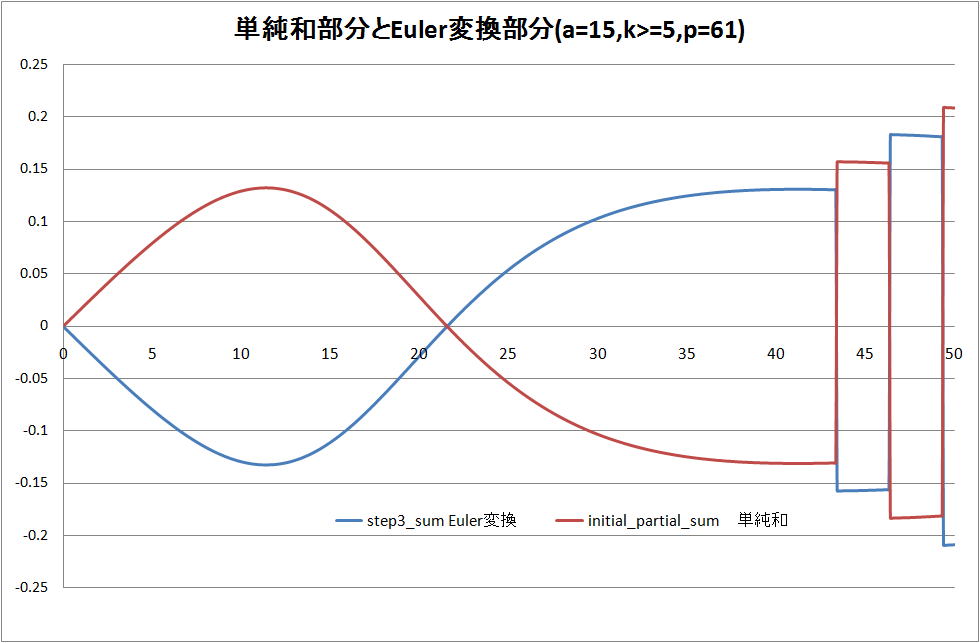
　　　　上図の43radianで、単純和とEuler変換部分の数値の正負が変化している。この時間はk値を増加
　　　　させた時間である。このように、各項の位相が正値の時に、k値を増加させると単純和とEuler変換
　　　　和の値の正負が変わり、発散、脱調が発生しない。
　　　　なお、失速/脱調時に、各項の位相が全て正になるのは、cosineであり、sineは、負になる。

　4)FILTの発散、脱調防止方法の具体的計算(コード3)
　　　　(1)計算対象
　　　　　 (s^3+2s^2+3s)/(s^4+2s^3+4s^2+2s^2+3)、 cosine

　　　　(2)k値増加
　　　　　仮にkを4個(jk=k+4,k=5)増加し、jk=9の単純和個所の9項の位相の算出。
　　　　　これで、位相が負になる項がなければ、更に4項を追加し、13項の位相を確認し、無ければ、
　　　　　初めて、k=k+1とする。増加させるｋの値4は、感覚的に決めた。
　　　　　 p=61,a=15である。
　　　　　計算回数繰り返し31995回、対象時間 2500 radian、cos(t)の波の数 398

　　　　(3)コード内の位相の正負の個数の算出方法
　　　　　コードのstep2_phaseを各項の位相とした時、隣の項に正負の変化があった場合には、隣と
　　　　　の積は必ず負になる。これを下記のSTLのtransformを使用し算出した。

　　　　　　vector<long double>v2(jk,0.0);
　　　　　　transform(step2_phase.begin(),step2_phase.end()-1,step2_phase.begin()+1,
　　　　　　　　　　　v2.begin(),multiplies<double>());

　　　　　また、負の個数算出は、STL/count_ifを使用した。

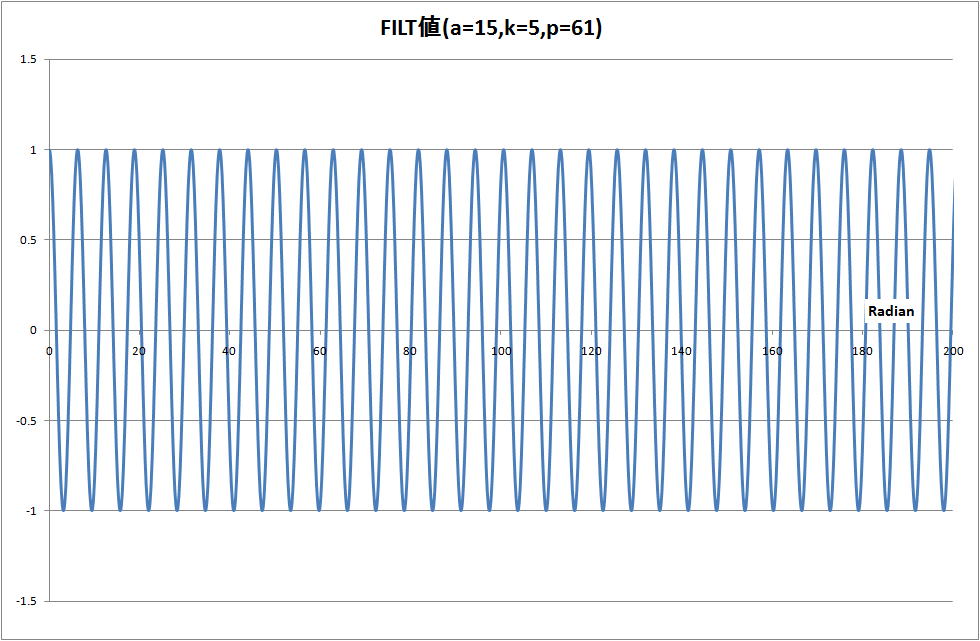
　　　　(4)計算結果　
　　　　　・発散、脱調はない。この結果を下図に示す。
　　　　　・計算精度　10-9乗

　　　　　

　　　

感想；細野氏や小池氏の時代は、言語の制約があり、複素数を自由に扱う事が出来なかった。
　　　現在は、STL/vectorの利用で、複素数計算が容易になり、コード記述が簡単になった。
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

このページの先頭へ

2、移動則

1、逆ラプラス変換(FILT)での移動則(コード4)
　1)移動則の説明
　　時間 t に a だけ遅れている関数をラプラス変換する場合は、時間軸を移動する方法となる。その
　　方法は、関数 f(t) が F(s) とラプラス変換されている時、時間を t-a とした時の変換である。
　　これを移動則という。のこぎり波等の表現に使われる。

　　この移動は、について以下のように変換する。

　　　　

　　　　　　　　　　

　　　　　　　　　　

　　　　結果として、ラプラス変換されたF(s)に、exp(-as)を掛ければ、時間軸が移動する事になる。

　2)逆ラプラス（FILT)での具体的な計算と結果(コード4)
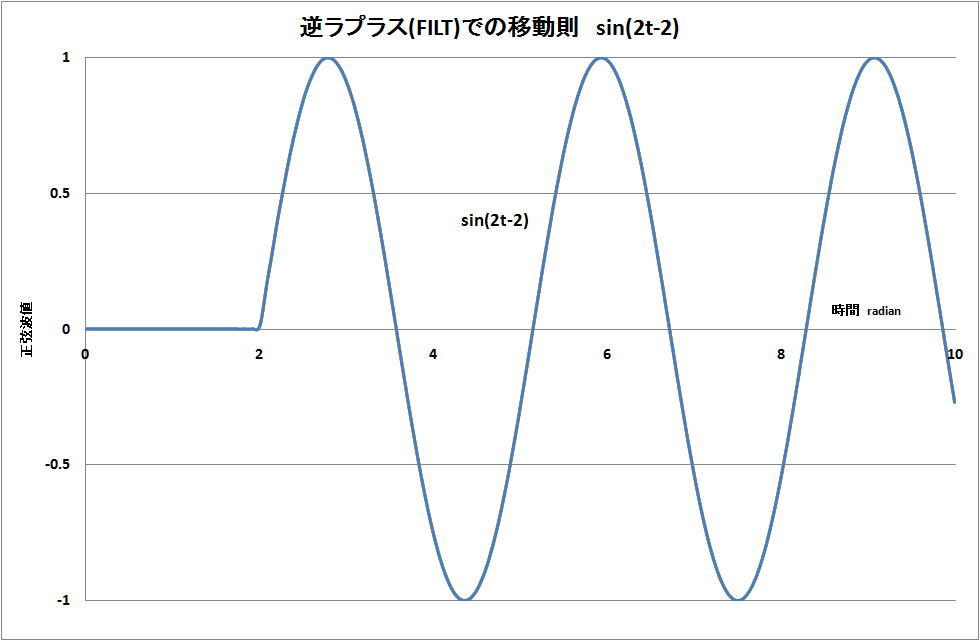
　　(1)計算の対象　　　　原関数 f(t)=sin(2t) 、ラプラス変換　F(s)=2/(s^2+4)

　　(2)移動(時間遅れ）　　 a=2 (radian)、 (コードでは、move_a=2 で表示)
　　　　　　　　　　　　　で、(t-a) 即ち開始から 2 までの間、sin(2t) がゼロになる。

　　(3)コード上の処置
　　　FILTで、複素数 frac[3] に exp(-as) を掛けて、新たに frac[3] とし、虚数部を採る。

　　　　　　frac[3]=frac[3]*exp(-move_a*s); //軸移動計算個所
　　　　　　a[i]=sg*((imag(frac[3])));

　　(4)計算結果
　　　下図に示すように、y軸の値 f(t) が t の区間 0 から 2 までが 0.0 になっている。

　　　

2、結論
　逆ラプラス変換 (FILT) は、移動則を備えている。
　この事を細野氏、小池氏の本で、見出す事がまだ出来ていない。

3、使用したSTLと関数
　 array<double,4>a0、vector<complex<double>>pf(4,0.0)
　　　　　　　　　　　　　　　　　　　　　　　

このページの先頭へ

3、Bode Plot

1、Bode Plot ボード線図(コード5)
　制御では、各システムのボード線図( Bode Plot )が話題になる。ボード線図は、システムの周波数
　特性で、この算出は、ラプラス変換された P(s) で、s=jω と置き、P(s) を虚数部、実数部に分けて、
　ω が 0.1 から 10 まで動く時に、システムの絶対値の 20・log|P(s)| と位相の変化を求める計算で
　ある。

　1)Bode Plot ボード線図作成上の考え方
　　逆ラプラス変換(FILT)の理論式は、逆ラプラス変換の節に記載した下記の式である。

　　　　　　

　　この式で、実数 a をゼロにすると、逆ラプラス変換の計算が、虚数 j 項だけの計算となる。この状
　　態で、(n-0.5)の 0.5 をゼロにすると、ｎと t で、虚数部の計算が出来て、Bode Plot が得られる。

　2)計算の説明
　　(1)計算対象
　　　 1/(s^2+2s+3) の Bode Plot

　　(2)計算結果
　　　下図に示す。
　　　　
　　
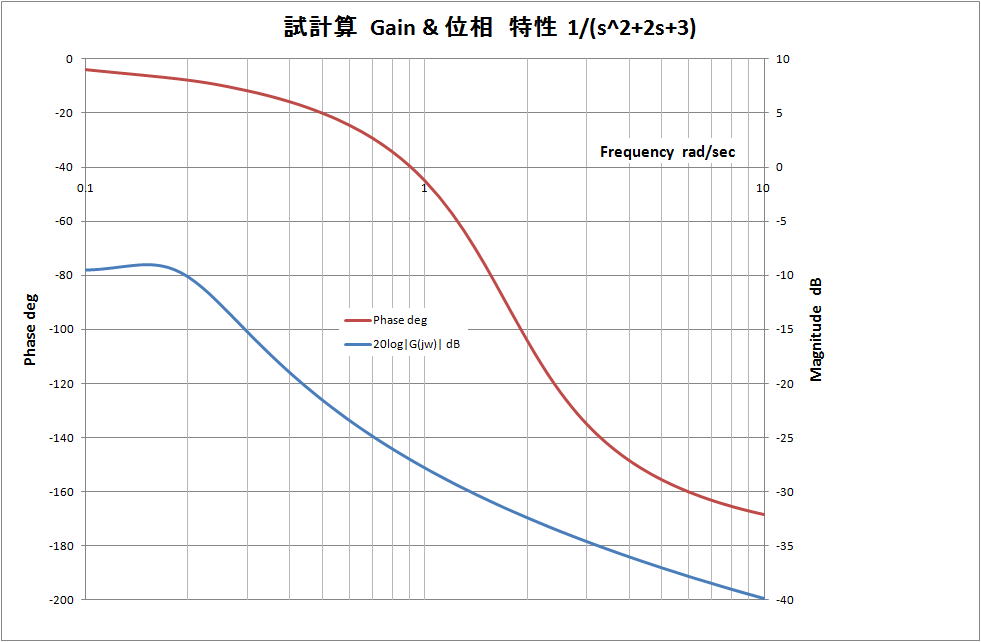
　　(3)結果について
　　　コードの試計算で、下記の参考文献"MATLABによる制御工学"のPage 63 にある1/(s^2+s+1)
　　　の場合を計算した。両者のボード線図は同じであった。
　　　従い、計算コードの考えは、妥当である。

2、Feedbac回路計算の一部機能利用計算とボード線図専用計算の比較
　　Feedback回路計算の一部機能利用とは、次章の第6章に示している計算コードの機能利用、すなわ
　　ち、パラメータのとり方を意味する。
　　c++ で、発散・失速対策を施した本章の逆ラプラス変換計算をFeedback回路に適用した計算方法
　　でも、Bode Plot の計算が出来る事を示す。コードの具体的な詳細は、次章第6章に示す。

　1)計算の説明
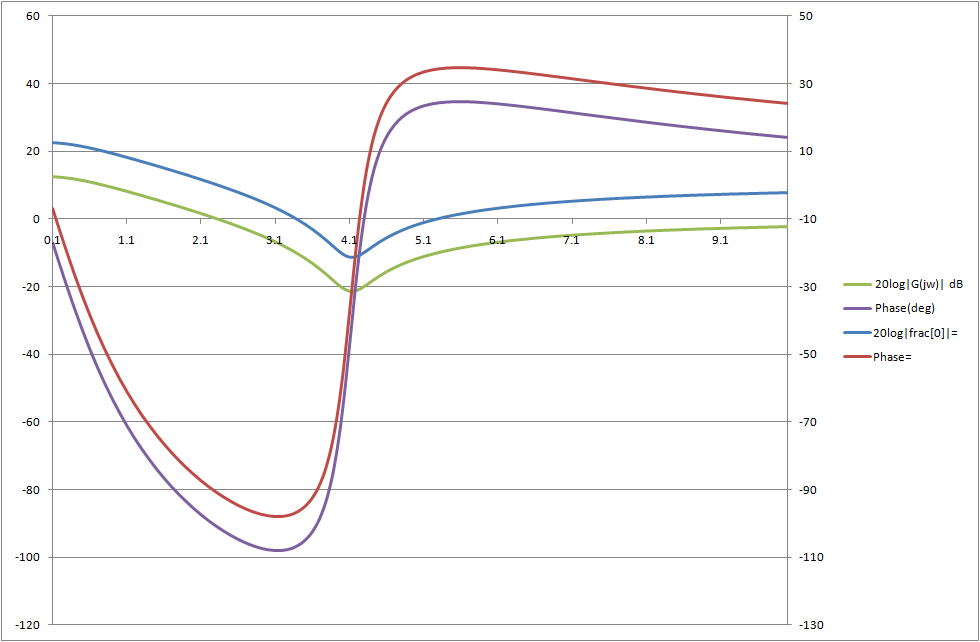
　　(1)計算対象　(s^2+0.5s+17)/(s^2+5.0s+4)

　　(2)計算結果
　　　両コード(Feedback回路計算とBode Plot専用)の比較計算結果を下図に示す。
　　　黄緑と青の中央が谷の曲線が 20log10|G(jω)| を示す。赤と紫の降下上昇の曲線が位相を示す。
　　　両コードの曲線は、左右の軸で、10 dBあるいは10度の差を設けて表示している。
　　　両者、同じであるので、逆ラプラス変換の計算内のBode Plotの計算に誤りが無い事になる。

　　　　　

3、使用したSTLと関数
　　array<double,n>、vector<complex<double>>、fraction[2].real(real(data))、arg(frac[0])

4、参考文献
　　・"演習で学ぶPID制御"　森泰親著、東北出版　2009年11月
　　・"MATLABによる制御工学"、足立修一著、東京電機大学出版

5、感想
　逆ラプラス変換 (FILT) で、Bodeplot が可能な事を細野氏、小池氏の本で、まだ、見出していない。
　これは、細野氏や小池氏の時代は、言語の制約があり、複素数を自由に扱う事が出来なかった事に
　よる。しかし、現在は、STL/vectorの利用で複素数計算が容易になり、コード記述が簡単になった。

Information

2012年: この章の全体履歴
2012年1月7日　再公開　
2012年: この章の変更追加履歴
1) 写真の追加 2012_8_29

このページの先頭へ

_________________________＿＿＿＿__＿＿＿_____＿＿＿_______計算コードの具体例____________________________________________
1、逆ラプラス変換(コード1)　FILTによる計算　(安定系)
#include <fstream>
#include <complex>
#include <cmath>
#include <vector>
#include <iomanip>
using namespace std;

const double PI=3.14159265358979323846264338327950288;
const complex<double> real_unit(1.0,0),imag_unit(0.0,1.0);

void reverse(int,double*,int,double*,double,double,double,double,double*,double*);

int main()
{
int n,m;
double a1[10],b1[10];
double filt_a,t,k1,k2;
double y,z;
int repeat_time;

//* cosineの場合 ( s^3 + 2s^2 + 3s + 0 )/( s^4 + 2s^3 + 4s^2 + 2s + 3) = s/(s^2 + 1 )

n=3; //分子の次数
a1[0]=0;
a1[1]=3;
a1[2]=2;
a1[3]=1;
m=4; //分母の次数
b1[0]=3;
b1[1]=2;
b1[2]=4;
b1[3]=2;
b1[4]=1;
filt_a=20.0;//exp(filt_a)の値
k1=5;
k2=0.5;

t=0.078539816339745;//刻みピッチ
repeat_time=90;//繰返数、これを大きくすれば曲線の横軸が大。

n++;
m++;
double tj;

ofstream out1("output_reverse_Laplace.csv" ,ios::out |ios::binary );
out1<<" Euler変換次数 p ="<<","<<61<<","<<" filt_a="<<','<<filt_a<<endl;
out1<<"tj"<<","<<"y"<<","<<"cos(tj)"<<','<<"y-cos(tj)" <<","<<"filt_trancation"<<endl;

for (int j=1;j<repeat_time;j++)
{
tj=t*j;

reverse(n,a1,m,b1,filt_a,k1,k2,tj,&y,&z);

out1<<setprecision(20)<<tj<<","<<setprecision(20)<<y<<","<<setprecision(20)<<cos(tj)
<<','<<setprecision(20)<<y-cos(tj)<<","<<setprecision(20)<<z<<endl;
}
out1.close();
return 0;
}

// function文 reverse
void reverse(int n,double *a1,int m,double *b1, double filt_a,double k1,double k2,double t,double *y,double *z)
{
complex<double> s;
vector<complex<double>>numerator(1,(0.0,0.0));
vector<complex<double>>denominator(1,(0.0,0.0));

double initial_partial_sum=0.0;
double sg=-1.0;//-1はFILTのΣの最初がマイナスであるため。Σ(-1)^n×Im(F(s)),(n=1,2,3…)

int i,j,k;
k=(int)(k1+t*k2);//この始めのeuler変換を行わない項が変化する。

//始めの数項をFILTの定義でそのまま計算

for(i=1;i<=k;i++) //Σ(-1)^n×Im(F(s)),(n=1,2,3…)は1から始めるので、i=1からkまで。　
{
s=filt_a/t*real_unit+(i*PI/t-PI/t/2.0)*imag_unit;

numerator[0]=(0.0,0.0);//vector利用時、v[0]=v[0]+xxxが可能。
for(j=n;j>0;j--) numerator[0]=numerator[0]+a1[j-1]*pow(s,j-1);
denominator[0]=(0.0,0.0);
for(j=m;j>0;j--) denominator[0]=denominator[0]+b1[j-1]*pow(s,j-1);

initial_partial_sum+=sg*imag(numerator[0]/denominator[0]);
sg=-sg;
}

vector<double>a(61+1,(0.0));//61次のeuler変換ための配列を61個作成

for(i=0;i<=61;i++)//前にkまでの和を算出。euler変換用a[0]のためi=0でスタート。
{
s=filt_a/t*real_unit+((i+k+1)*PI/t-PI/t/2.0)*imag_unit;//(i+k+1)で始める。

numerator[0]=(0.0,0.0);
for(j=n;j>0;j--) numerator[0]=numerator[0]+a1[j-1]*pow(s,j-1);
denominator[0]=(0.0,0.0);
for(j=m;j>0;j--) denominator[0]=denominator[0]+b1[j-1]*pow(s,j-1);

a[i]=sg*imag(numerator[0]/denominator[0]);
sg=-sg;
}

double step3_sum=(1*a[61]+63*a[60]+1954*a[59]+39774*a[58]+597619*a[57]+7068621*a[56]+68543140*a[55]+560339292*a[54]
// 以下　第 6 章のEuler変換をご参照ください。

// 以上　第 6 章のEuler変換をご参照ください。
+4611686018427387841*a[1]+4611686018427387903*a[0])/4611686018427387904;

double filt_value=exp(filt_a)/t*(step3_sum+initial_partial_sum);//求める解の値
*y=filt_value;

//誤差 trancation error euler打ち切り誤差

double euler_trancation=fabs(a[0]+61*a[1]+1830*a[2]+35990*a[3]+521855*a[4]+5949147*a[5]+55525372*a[6]+436270780*a[7]
// 以下　第 6 章のEuler変換をご参照ください。

//以上　第 6 章のEuler変換をご参照ください。
+436270780*a[54]+55525372*a[55]+5949147*a[56]+521855*a[57]+35990*a[58]+1830*a[59]+61*a[60]+1*a[61])/2305843009213693952;

double filt_trancation=exp(filt_a)/t*euler_trancation;
*z=filt_trancation;

}

本章の説明へ

2、逆ラプラス変換（コード2）　FILTによる計算　（拡大系）
#include <fstream>
#include <complex>
#include <cmath>
#include <vector>
using namespace std;

const double PI=3.14159265358979323846264338327950288;
const complex<double> real_unit(1.0,0),imag_unit(0.0,1.0);

void reverse(int,double*,int,double*,double,double,double,double,double*,double*,double);

int main()
{
int n,m;
double a1[10],b1[10];
double filt_a,t,k1,k2;
double y,z;
int repeat_time;
double b;

// 入力 1/( s^2 -2s^2 + 2 ) ( = exp(b*t)*sin(t) )

n=0; //分子の次数
a1[0]=1.0;
m=2;//分母の次数
b1[0]=2.0;
b1[1]=-2.0;
b1[2]=1.0;
filt_a=5.0;//exp(a)のa値
k1=20;
k2=1.6;
t=0.078539816;//刻みピッチ
repeat_time=1000;//繰返数、
b=1.0;//分母の実数解

//p=61;//euler変換

n++;
m++;
double tj;

ofstream out1("output_reverse_Laplace.csv" ,ios::out |ios::binary );
out1<<" Euler変換次数 p="<<","<<61<<","<<" filt_a="<<','<<filt_a<<","<<"b= "<<","<<b<<endl;
out1<<"tj"<<","<<"y"<<","<<"exp(b*tj)*sin(tj)"<<','<<"(y-exp(b*tj)*sin(tj)/exp(b*tj)*sin(tj)"<<","<<"filt_trancation"<<endl;

for (int j=1;j<repeat_time;j++)
{
tj=t*j;

reverse(n,a1,m,b1,filt_a,k1,k2,tj,&y,&z,b);

out1<<tj<<","<<y<<","<<exp(b*tj)*sin(tj)<<","<<(y-exp(b*tj)*sin(tj))/exp(b*tj)*sin(tj)<<","<<z<<endl;
}
out1.close();
return 2012;
}

// function文 reverse
void reverse(int n,double *a1,int m,double *b1, double filt_a,double k1,double k2,double time,double *y,double *z,double b)
{
complex<double> s;
vector<complex<double>>numerator(1,(0.0,0.0));
vector<complex<double>>denominator(1,(0.0,0.0));

double initial_partial_sum=0.0;
double sg=-1.0;//-1はFILTのΣの最初がマイナスであるため。

int i,j,k;
k=(int)(k1+time*k2);

//第一ステップ　始めの数項をFILTの定義で計算
for(i=1;i<=k;i++) //Σ(-1)^n×Im(F(s)),(n=1,2…)は1から始まるので、i=1から。　
{
s=(filt_a/time+b)*real_unit+(i*PI/time-PI/time/2.0)*imag_unit;//b項追加

numerator[0]=(0.0,0.0);
for(j=n;j>0;j--) numerator[0]=numerator[0]+a1[j-1]*pow(s,j-1);
denominator[0]=(0.0,0.0);
for(j=m;j>0;j--) denominator[0]=denominator[0]+b1[j-1]*pow(s,j-1);

initial_partial_sum+=sg*imag(numerator[0]/denominator[0]);
sg=-sg;
}

//第二ステップ　 Euler transform
vector<double>a(61+1,(0.0));//Euler変換ための配列を61+1個作成

for(i=0;i<=61;i++)//euler変換用a[0]のためi=0でスタート。
{
s=(filt_a/time+b)*real_unit+((i+k+1)*PI/time-PI/time/2.0)*imag_unit;//(i+k+1)。

numerator[0]=(0.0,0.0);
for(j=n;j>0;j--) numerator[0]=numerator[0]+a1[j-1]*pow(s,j-1);
denominator[0]=(0.0,0.0);
for(j=m;j>0;j--) denominator[0]=denominator[0]+b1[j-1]*pow(s,j-1);

a[i]=sg*imag(numerator[0]/denominator[0]);
sg=-sg;
}

double step3_sum=(double)(1*a[61]+63*a[60]+1954*a[59]+39774*a[58]+597619*a[57]
// 以下　第 6 章の Euler変換をご参照ください。

// 以上　第 6 章の Euler変換をご参照ください。
+4611686018427387903*a[0])/4611686018427387904;

//求める解の値
double filt_value=exp(filt_a+b*time)/time*(step3_sum+initial_partial_sum);
*y=filt_value;

double euler_trancation=fabs(a[0]+61*a[1]+1830*a[2]+35990*a[3]
// 以下　第 6 章の Euler変換をご参照ください。

// 以上　第 6 章の Euler変換をご参照ください。
+61*a[60]+1*a[61])/2305843009213693952;

double filt_trancation=exp(filt_a+b*time)/time*euler_trancation;
*z=filt_trancation;
}

本章の説明へ

3、FILTの発散、脱調防止方法の具体的計算(コード3)
#include <fstream>
#include <complex>
#include <cmath>
#include <vector>
#include <algorithm>
#include <functional>
using namespace std;

bool minusvalue(double xx) { if(xx<0.0) return true; return false; }

const double PI=3.14159265358979323846264338327950288;
const complex<double>real_unit(1.0,0),imag_unit(0.0,1.0);//複素数化

void k_control(int,double*,int,double*,double,int,double,double*,int*,int*);

void reverse(int,double*,int,double*,double,int,double,double*,double*);

int main()
{
int n; //分子の次数
double a1[10]; //分子の係数
int m; //分母の次数
double b1[10]; //分母の係数
int k1; //交代級数の単純和部分の項数
//int p=61; //Euler変換の次数
double filt_a; //FILTのexp(a)のa
double t; //ピッチ幅
int repeat_time;//計算の繰り返し数とピッチ幅で、時間

//計算対象　計算対象 ( s^3 + 2s^2 + 3s )/( s^4 + 2s^3 + 4s^2 + 2s^2 + 3 )、 cos(t)
n=3;
a1[0]=0.0;
a1[1]=3.0;
a1[2]=2.0;
a1[3]=1.0;

m=4;
b1[0]=3.0;
b1[1]=2.0;
b1[2]=4.0;
b1[3]=2.0;
b1[4]=1.0;

filt_a=15;
k1=5;
t=0.078539816339745;
repeat_time=10000;

n++;
m++;
double y; //求める値
double z; //打切誤差
double tj;//時間(radian)
int k,kk,mm=0;
vector<int>kj(repeat_time,0);
kj[0]=k1; //kjは一つ前の単純和の項数保持

ofstream out1("out_FILT.csv" ,ios::out |ios::binary );
out1<<" FILTによる逆ラプラス変換の値 "<<endl;
out1<<" Euler変換の次数 ="<<61<<","<<" filt_a="<<filt_a<<endl;
out1<<"time"<<","<<"求値y"<<","<<"cos t"<<','<<"打切"<<","<<"k"<<endl;

for (int j=1;j<repeat_time;j++)
{
tj=t*j; //tjは開始からの時間
if(mm==1) {k1=kj[j-1];mm=mm+1;} //k値保持
k_control(n,a1,m,b1,filt_a,k1,tj,&y,&mm,&kk);//k値制御部分
kj[j]=kk;
if(kj[j]<kj[j-1]) kj[j]=kj[j-1];
k=kj[j];
reverse(n,a1,m,b1,filt_a,k,tj,&y,&z);
out1<<tj<<","<<y<<","<<cos(tj)<<","<<z<<","<<k<<endl;
}
out1.close();

return 0;
}

// function文
void k_control(int n,double *a1,int m,double *b1, double filt_a,int k1,double time, double *y,int *mm,int *kk )
{
complex<double> s;
vector<complex<double>>numerator(1,(0.0,0.0));
vector<complex<double>>denominator(1,(0.0,0.0));
double initial_imag_sum=0.0;
double initial_real_sum=0.0;
int i,j,k;
k=k1;

vector<double>step1_phase(k+1,0.0);
for(i=1;i<=(k+1);i++) //k+1個の計算は、隣合わせの積を最終的にk個作るため。
{
s=filt_a/time*real_unit+(i*PI/time-PI/time/2.0)*imag_unit;
numerator[0]=(0.0,0.0);
for(j=n;j>0;j--) numerator[0]=numerator[0]+a1[j-1]*pow(s,j-1);
denominator[0]=(0.0,0.0);
for(j=m;j>0;j--) denominator[0]=denominator[0]+b1[j-1]*pow(s,j-1);
initial_imag_sum=imag(numerator[0]/denominator[0]);
initial_real_sum=real(numerator[0]/denominator[0]);
step1_phase[i-1]=atan(initial_real_sum/initial_imag_sum);
}

vector<double>v1(k+1,0.0);//k+1個の代入でtransform計算。
transform(step1_phase.begin(),step1_phase.end()-1,step1_phase.begin()+1,v1.begin(),multiplies<double>());

int jk=0;
int kn=4; //初期項数に追加する項数 knの4は感である。
int minus_data=0; //下記v1.end()-1で k+1-1=k個での位相変化を調査。
minus_data=(int)count_if(v1.begin(),v1.end()-1,bind2nd(less<double>(),0.0));
*mm=0;
if(minus_data==0)
{
*mm=*mm+1; //位相変化個所が無い時、mm=0でmainに戻される。
jk=k+kn;
}

//単純和の項数kを増やしたくないので位相を再度調査
initial_imag_sum=0.0;
initial_real_sum=0.0;
vector<double>step2_phase(jk+1,0.0);
for(i=1;i<=(jk+1);i++)
{
s=filt_a/time*real_unit+(i*PI/time-PI/time/2.0)*imag_unit;
numerator[0]=(0.0,0.0);
for(j=n;j>0;j--) numerator[0]=numerator[0]+a1[j-1]*pow(s,j-1);
denominator[0]=(0.0,0.0);
for(j=m;j>0;j--) denominator[0]=denominator[0]+b1[j-1]*pow(s,j-1);
initial_imag_sum=imag(numerator[0]/denominator[0]);
initial_real_sum=real(numerator[0]/denominator[0]);
step2_phase[i-1]=atan(initial_real_sum/initial_imag_sum);
}

vector<double>v2(jk+1,0.0);
transform(step2_phase.begin(),step2_phase.end()-1,step2_phase.begin()+1,v2.begin(),multiplies<double>());
int minus_data0=0;
minus_data0=(int)count_if(v2.begin(),v2.end()-1,bind2nd(less<double>(),0.0));
if(minus_data0 ==0) jk=k+kn+kn;

//単純和の項数kを増やしたくないので位相を再々度調査
initial_imag_sum=0.0;
initial_real_sum=0.0;
vector<double>step3_phase(jk+1,0.0);
for(i=1;i<=(jk+1);i++)
{
s=filt_a/time*real_unit+(i*PI/time-PI/time/2.0)*imag_unit;
numerator[0]=(0.0,0.0);
for(j=n;j>0;j--) numerator[0]=numerator[0]+a1[j-1]*pow(s,j-1);
denominator[0]=(0.0,0.0);
for(j=m;j>0;j--) denominator[0]=denominator[0]+b1[j-1]*pow(s,j-1);
initial_imag_sum=imag(numerator[0]/denominator[0]);
initial_real_sum=real(numerator[0]/denominator[0]);
step3_phase[i-1]=atan(initial_real_sum/initial_imag_sum);
}

vector<double>v3(jk+1,0.0);
transform(step3_phase.begin(),step3_phase.end()-1,step3_phase.begin()+1,v3.begin(),multiplies<double>());
int minus_data1=0;
minus_data1=(int)count_if(v3.begin(),v3.end()-1,bind2nd(less<double>(),0.0));
if(minus_data1 ==0) k=k+1;

*kk=k;
return;
}

// function文 reverse
void reverse(int n,double *a1,int m,double *b1, double filt_a,int k,double time, double *y,double *z)
{
complex<double> s;
vector<complex<double>>numerator(1,(0.0,0.0));
vector<complex<double>>denominator(1,(0.0,0.0));

double initial_partial_sum=0.0;
double sg=-1.0;
int i,j;

//第一ステップ　始めの数項をFILTの定義で計算
for(i=1;i<=k;i++)
{
s=filt_a/time*real_unit+(i*PI/time-PI/time/2.0)*imag_unit;
numerator[0]=(0.0,0.0);
for(j=n;j>0;j--) numerator[0]=numerator[0]+a1[j-1]*pow(s,j-1);
denominator[0]=(0.0,0.0);
for(j=m;j>0;j--) denominator[0]=denominator[0]+b1[j-1]*pow(s,j-1);
initial_partial_sum+=sg*imag(numerator[0]/denominator[0]);
sg=-sg;
}

// Euler transformer
vector<double>a(61+1,(0.0));//euler変換の配列
for(i=0;i<=61;i++)//k項からEuler変換の和を求める。i=0故、(i+k+1)で始める。
{
s=filt_a/time*real_unit+((i+k+1)*PI/time-PI/time/2.0)*imag_unit;
numerator[0]=(0.0,0.0);
for(j=n;j>0;j--) numerator[0]=numerator[0]+a1[j-1]*pow(s,j-1);
denominator[0]=(0.0,0.0);
for(j=m;j>0;j--) denominator[0]=denominator[0]+b1[j-1]*pow(s,j-1);
a[i]=sg*imag(numerator[0]/denominator[0]);
sg=-sg;
}

double step3_sum=(double)(1*a[61]+63*a[60]+1954*a[59]+39774*a[58]+
// 以下　第 6 章のEuler変換をご参照ください。

// 以上　第 6 章のEuler変換をご参照ください。
4611686018427387903*a[0])/4611686018427387904;

double filt_value=exp(filt_a)/time*(step3_sum+initial_partial_sum);
*y=filt_value;// 求める値

//誤差 trancation error euler打ち切り誤差
double euler_trancation=(double)fabs(a[0]+61*a[1]+1830*a[2]+
//　以下　第 6 章のEuler変換をご参照ください。

//　以上　第 6 章のEuler変換をご参照ください。
35990*a[58]+1830*a[59]+61*a[60]+1*a[61])/2305843009213693952;

double filt_trancation=exp(filt_a)/time*euler_trancation;
*z=filt_trancation;
return;
}

本章の説明へ

4、逆ラプラス変換(FILT)での移動則(コード4)
#include <fstream>
#include <complex>
#include <cmath>
#include <vector>
#include <algorithm>
#include <functional>
using namespace std;
#include <array>
using namespace std::tr1;

const double PI=3.14159265358979323846264338327950288;
const complex<double>real_unit(1.0,0),imag_unit(0.0,1.0);

void reverse(array<double,4>,array<double,4>,array<double,4>,array<double,4>,array<double,4>,array<double,4>,
       array<double,4>,array<double,4>,float,double,double,int,double,double*,double);

int main()
{
//移動演算子 exp(-move_a*s)で、move_a/nick回数を移動する。

array<double,4> a0={1.0,0.0,0.0,0.0};
array<double,4> a1={1.0,0.0,0.0,0.0};
array<double,4> b0={1.0,0.0,0.0,0.0};
array<double,4> b1={1.0,0.0,0.0,0.0};
array<double,4> c0={1.0,0.0,0.0,0.0};
array<double,4> c1={1.0,0.0,0.0,0.0};
array<double,4> d0={1.0,0.0,0.0,0.0};
array<double,4> d1={1.0,0.0,0.0,0.0};

double move_a=2.00;//軸移動パラメータ

float feedwith=0.0; //Feedback回路有：1.0　無：0.0

//対象 2/(s^2+4) sin(2*t)を移動move_aで2.0/nickまで0。　

a0[0]=2.0;
b0[0]=4.0;
b0[1]=0.0;
b0[2]=1.0;

double filt_a=15;  // FILTの精度パラメータ
double nick=0.01;  //刻みpitch
int k1=6;          //FILTの初期項計算の項数
//int p=61;        //Euler変換項数、次数
int repeat_no=1000;//計算域となる繰返し数
double b=0.0;      //通常はゼロ。実数

double y;
double time;

ofstream out1("FILT_move.csv",ios::out|ios::binary);
out1<<" FILTによる逆ラプラス変換の値 "<<endl;
out1<<" Euler変換次数 = "<<61<<","<<" filt_a="<<filt_a<<endl;
out1<<" j"<<","<<"time (radian)"<<","<<"求値 y"<<","<<"k"<<endl;

for (int j=1;j<repeat_no;j++)
{
time=nick*j;//timeは開始からの時間
reverse(a0,b0,a1,b1,c0,d0,c1,d1,feedwith,move_a,filt_a,k1,time,&y,b);
out1<<j<<","<<time<<","<<y<<","<<k1<<endl;
}
out1.close();
return 0;
}

// function文 reverse
void reverse(
array<double,4>a0,array<double,4>b0,array<double,4>a1,array<double,4>b1,array<double,4>c0,array<double,4>d0,
array<double,4>c1,array<double,4>d1,float feedwith,double move_a,double filt_a,int k,double time,double *y,double b)
{
complex<double> s;
double initial_partial_sum=0.0;
int max_j=4;
vector<complex<double>>pf(max_j,(0.0,0.0));
vector<complex<double>>nume1(4,(0.0,0.0));
vector<complex<double>>deno1(4,(0.0,0.0));
vector<complex<double>>frac(4,(0.0,0.0));
double sg=-1.0;
int i;

//第一ステップ　始めの数項をFILTの定義で計算
for(i=1;i<=k;i++)
{
s=(filt_a/time+b)*real_unit+PI/time*(i-0.5)*imag_unit;
pf[0]=real_unit;
for(int jj=1;jj<max_j;jj++) pf[jj]=pow(s,jj);

nume1[0]=(a0[0]*pf[0]+a0[1]*pf[1]+a0[2]*pf[2]+a0[3]*pf[3])*(a1[0]*pf[0]+a1[1]*pf[1]+a1[2]*pf[2]+a1[3]*pf[3]);
deno1[0]=(b0[0]*pf[0]+b0[1]*pf[1]+b0[2]*pf[2]+b0[3]*pf[3])*(b1[0]*pf[0]+b1[1]*pf[1]+b1[2]*pf[2]+b1[3]*pf[3]);

nume1[1]=(c0[0]*pf[0]+c0[1]*pf[1]+c0[2]*pf[2]+c0[3]*pf[3])*(c1[0]*pf[0]+c1[1]*pf[1]+c1[2]*pf[2]+c1[3]*pf[3]);
deno1[1]=(d0[0]*pf[0]+d0[1]*pf[1]+d0[2]*pf[2]+d0[3]*pf[3])*(d1[0]*pf[0]+d1[1]*pf[1]+d1[2]*pf[2]+d1[3]*pf[3]);

frac[0]=(0.0,0.0);
frac[1]=(0.0,0.0);
frac[2]=(0.0,0.0);
frac[3]=(0.0,0.0);

frac[0]=nume1[0]/deno1[0];
frac[1]=nume1[1]/deno1[1];
frac[2]=(double)feedwith*frac[1];
frac[3]=frac[0]/(1.0*real_unit+frac[2]);

//以下検討中

//以上検討中
}

// Euler transformer
vector<double>a(61+1,(0.0));//euler変換の配列
for(i=0;i<=61;i++)//i=0であるので、(i+k+1)で始める。
{
s=(filt_a/time+b)*real_unit+PI/time*(i+k+0.5)*imag_unit;
pf[0]=real_unit;
for(int jj=1;jj<max_j;jj++) pf[jj]=pow(s,jj);

nume1[0]=(a0[0]*pf[0]+a0[1]*pf[1]+a0[2]*pf[2]+a0[3]*pf[3])*(a1[0]*pf[0]+a1[1]*pf[1]+a1[2]*pf[2]+a1[3]*pf[3]);
deno1[0]=(b0[0]*pf[0]+b0[1]*pf[1]+b0[2]*pf[2]+b0[3]*pf[3])*(b1[0]*pf[0]+b1[1]*pf[1]+b1[2]*pf[2]+b1[3]*pf[3]);

nume1[1]=(c0[0]*pf[0]+c0[1]*pf[1]+c0[2]*pf[2]+c0[3]*pf[3])*(c1[0]*pf[0]+c1[1]*pf[1]+c1[2]*pf[2]+c1[3]*pf[3]);
deno1[1]=(d0[0]*pf[0]+d0[1]*pf[1]+d0[2]*pf[2]+d0[3]*pf[3])*(d1[0]*pf[0]+d1[1]*pf[1]+d1[2]*pf[2]+d1[3]*pf[3]);

frac[0]=(0.0,0.0);
frac[1]=(0.0,0.0);
frac[2]=(0.0,0.0);
frac[3]=(0.0,0.0);

frac[0]=nume1[0]/deno1[0];
frac[1]=nume1[1]/deno1[1];
frac[2]=(double)feedwith*frac[1];
frac[3]=frac[0]/(1.0*real_unit+frac[2]);

frac[3]=frac[3]*exp(-move_a*s);//軸移動計算個所

a[i]=sg*((imag(frac[3])));
sg=-sg;
}

double step3_sum=(double)(1*a[61]+63*a[60]
// 以下　第 6 章の Euler変換をご参照ください。

// 以上　第 6 章の Euler変換をご参照ください。
+4611686018427387841*a[1]+4611686018427387903*a[0])/4611686018427387904;

double filt_value=exp(filt_a+b*time)/time*(step3_sum+initial_partial_sum);
*y=filt_value;// 求める値
return;
}

本章の説明へ

5、Bode Plot ボード線図(コード5)
#include <fstream>
#include <complex>
#include <vector>
using namespace std;
#include <array>
using namespace std::tr1;

const double PI=3.14159265358979323846264338327950288;
const complex<double>real_unit(1.0,0),imag_unit(0.0,1.0);

int main()
{
array<double,8> a0={1.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0};
array<double,8> b0={1.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0};

//Phase_plot calculation data 1/(s^2+2s+3)
a0[0]=1.0;
b0[0]=3.0;
b0[1]=2.0;
b0[2]=1.0;

int max_j=8;
vector<complex<double>>pf(max_j,(0.0,0.0));
vector<complex<double>>nume1(1,(0.0,0.0));
vector<complex<double>>deno1(1,(0.0,0.0));
vector<complex<double>>frac(1,(0.0,0.0));

double filt_a=0.00;
complex<double> s;
double time=PI/0.1;

ofstream out12("Bode_plot.csv" ,ios::out |ios::binary);
out12<<"i"<<","<<"Frequency rad/s"<<","<<"20log|G(jw)| dB"<<","<<"Phase deg"<<endl;

for(int i=1;i<=100;i++)
{
s=(filt_a/time)*real_unit+PI/time*i*imag_unit;//FILTの0.5を削除

pf[0]=real_unit;
for(int jj=1;jj<max_j;jj++) pf[jj]=pow(s,jj);

nume1[0]=(a0[0]*pf[0]+a0[1]*pf[1]+a0[2]*pf[2]+a0[3]*pf[3]+a0[4]*pf[4]+a0[5]*pf[5]+a0[6]*pf[6]+a0[7]*pf[7]);
deno1[0]=(b0[0]*pf[0]+b0[1]*pf[1]+b0[2]*pf[2]+b0[3]*pf[3]+b0[4]*pf[4]+b0[5]*pf[5]+b0[6]*pf[6]+b0[7]*pf[7]);

frac[0]=(0.0,0.0);
frac[0]=nume1[0]/deno1[0];
out12<<i<<","<<s.imag()<<","<<20*log10(abs(frac[0]))<<","<<180/PI*arg(frac[0])<<endl;

}
out12.close();
return 0;
}

本章の説明へ

風と翼 Windandwing は、c++の数値計算から風と翼の計算へを目的とした数値計算を行っています。

第5章 逆ラプラス変換、移動則、Bode Plot

１、逆ラプラス変換

2、移動則

3、Bode Plot

Information

ナビゲーション

風と翼 Windandwing は、c++の数値計算から風と翼の計算へ を目的とした数値計算を行っています。

第5章 逆ラプラス変換、移動則、Bode Plot

１、逆ラプラス変換

2、移動則

3、Bode Plot

Information

ナビゲーション

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　風と翼 Windandwing は、c++の数値計算から風と翼の計算へを目的とした数値計算を行っています。

第5章逆ラプラス変換、移動則、Bode Plot