風と翼 Windandwing は、c++の数値計算から風と翼の計算へ を目的とした数値計算を行っています。

第7章 直交関数(Legendre、Chebyshev、Bessel)、直交関数系級数展開
直交多項式として、Legendre多項式、Chebyshev多項式、ラゲル多項式、エルミット多項式、Bessel関数を挙げる事ができる。これらの多項式では、同次数以外の内積は zero になる。詳細は、下記、参考図書をご参照ください。これらの中で、以下の直交関数について、具体的に多項式を提示し、直交性確認と多項式級数展開の計算を行った。
1、Legendre多項式 34次まで、算出し、直交性確認を数値計算で行った。
直交性確認の数値計算(数値積分)の手法として、Legendre 、Chebyshev の重み付数値積分、Newton-Cotes法
(台形則、Simpson則、および離散系データ用数値積分の転用での数値積分)を用いた。
更に、各手法の優劣比較を行った。従い、2012年以前のHomepageに記載した内容より増加している。
2、Chebyshev多項式 35次まで、算出した。
なお、直交性確認計算は、x=cosθ への変換による数値計算である。
3、Bessel関数
この関数は、科学や工学で重要な関数である。この関数、Bessel関数 J0、J1、 J(2n+1)/2 の
微分 J'0、J'1、J'(2n+1)/2 の定積分値を、Jn の関係により、不等間隔の数値計算で算出した。
数値計算により直交性の確認を行う事は、高次の Jn の計算や級数の収束計算を伴い、時間を要するために、
(フーリエ積分式で計算を行えば良いかも知れないが)まだ、考えが進まない。
4、直交関数系 級数展開 Legendre 多項式による級数展開の係数算出
Legendre 多項式による Chebyshev 多項式および sin(πx) の級数展開
Chebyshev 多項式による Legendre 多項式および sin(πx + π/2) の級数展開
Legendre・Chebyshev 多項式による関数の Maclaurin 展開の係数算出
参考図書 伏見康治、赤井逸:直交関数系(増補版),共立出版,1987
Legendre多項式
1、Legendre多項式 (コード L-1 )・Legendre多項式は、電磁気学に出てくる式で、以下の三通りの式で示される。
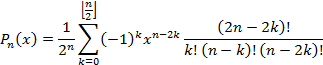 1-(1)式
1-(1)式・34次までのLegendre多項式の各次数毎の係数
各係数をコード L-1 に示す。34次では、コンパイラーの整数表示の制約のために少数表示の係数が有る。
これらの係数は、上記の式にあるように、係数の分母は2の n 乗になる。更に、多項式は、1-(1)式と漸化式
の1-(3)式で求めた。係数算出は、x の存在のために再帰法が使用出来ず、手計算で行った。
多項式の係数の検算は、結果的に、記載した多項式が数値計算により直交性を示す事で確認された。
2、直交性の数値的検証
・この多項式は、多くの書籍に示されているように、下記の直交性がある。
n=mの時、
n≠mの時
・数値計算で、m=nとm≠n (次数m,n)の直交性を確認した。計算法は、重み付き数値積分Gauss-Legendre、
Chebyshev、台形則等のNewton-Cotesである。
なお、直交性確認のための数値積分の計算で、不均等間隔の離散データ用の数値積分の計算結果は、
区間 [-1、1] の分割数が大きくなると、下表に示すように、正常な計算結果を示す積分式の次数が低下する
事象が生じた。
下表は、不均等間隔の離散データ用の数値積分についてのみの記述で、分割数 2 の時、積分式の次
数 10 の場合には、Pn・Pn (n=5) 以下が 1.0 と算出された事を示す。n≠ m の時は、積分式 10 次以下の
全てが、0.01であっても、ゼロとみなせるという計算結果を示している。分割数が大きくなると、計算精度
が高くなり、積分式の次数が 10 のままで、被積分の Legendre 多項式の次数が大きくなるのが通常と考え
られるが、下表はそうではない。
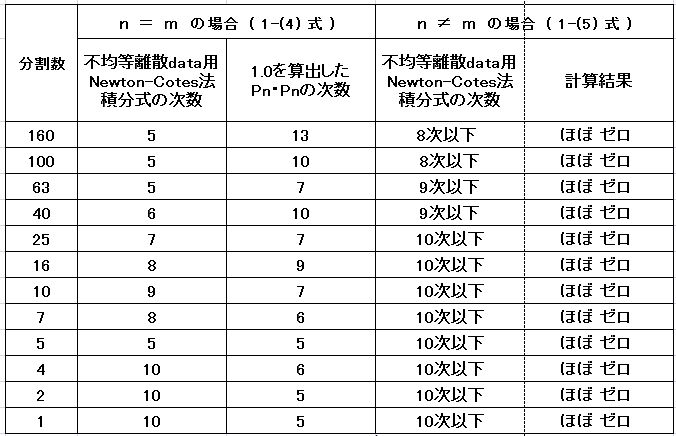
分割数 160 は、10次の積分式では、160 の 10 倍の 1600 のデータから算出する。9次の積分式は、9倍
の 1440 のデータから算出する事になる。これらの積分式の具体的な式は、数値計算 7 に記載するが、次数
が高くなると非常に計算の項数が増加し、誤差の蓄積が増加するために、前記のような不本意な結果になっ
たと考える。これは、計算の bit 数が増加すれば、解消できるのではないかと考える。
これでは、直交性を数値計算で確認すると言う本来の目的を達成できないので、不等間隔あるいは不均等
間隔の離散データ用の数値積分の計算結果を除外する。2012年以前のHomepageと同じ内容になる。
Gauss-Legendre 、Gauss-Chebyshev の重み付数値積分、Newton-Cotes法(等間隔)の数値積分の具体的
な次数は以下である。
Newton-Cotes法(等間隔) :台形則とSimpsonの1/3則、3/8則、Boole則、
Gauss-Legendre :2次、3次、4次、5次、6次
Gauss-Chebyshev :2次、3次、4次、5次、6次
2-1、対角要素 (コード L-2)
分割数により 1-(4)式を満足出来たPn(n次数)は コード L-2 で求めた。
[-1,1] 区間を分割数 1 ~ 25000 で適切に分割した結果を下図に示す。それぞれの積分手法を示す線の下方
が条件 2/(2m+1) を満足する次数である。
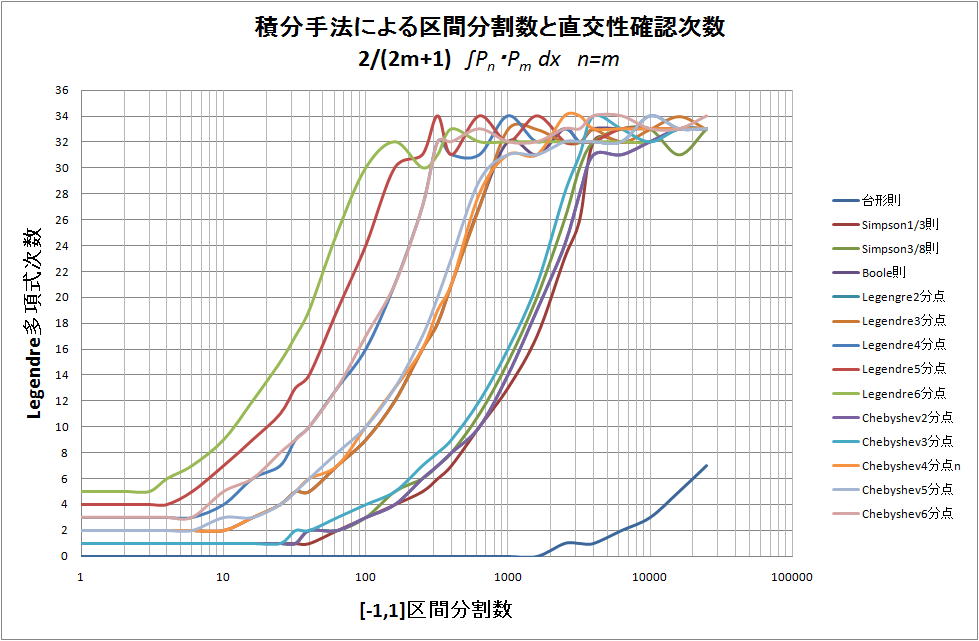
上図で、それぞれの積分手法(Simpson1/3~Chebyshev6分点)が分割数が増加しても多項式の31次と
34次間を32次を中心に振れているのは long double(64bit) の制約で数値計算の精度が悪くなっているため
である。long double が 128bit になれば、32次、33次、34次での飽和現象は生じず、もっと高い次数で
生じると考える。
また、上図は、6種のグループに分ける事ができる。最左の線は、Legendre6分点を、左の次の線は
Legendre5分点、最右の線は、台形則を示す。上図では、判りにくいので、図1と図2に分けて示す。
下図の図1は、Chebyshev6分点とLegendre4分点のグループ、Chebyshev3分点とLegendre2分点、
Chebyshev2分点、Simpson3/8則、Simpson3/8則のグループの二つのグループを示す。この図で判る
事は、Legendre4分点(4次)は、Chebyshev6分点(6次)と同じ精度で計算できる事である。
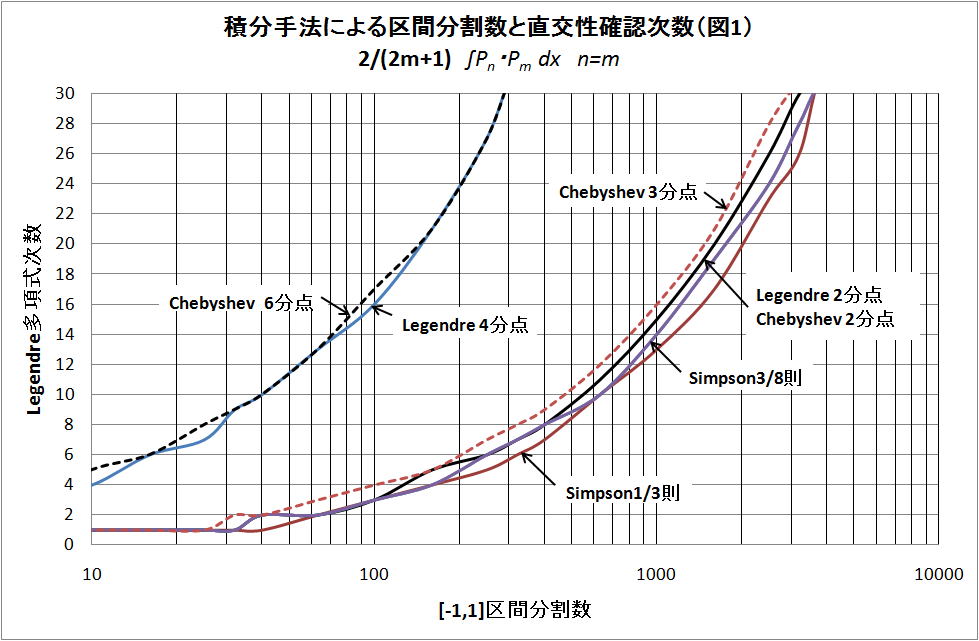
図2は、Legendre6分点、Legendre5分点、Chebyshev5分点とChebyshev4分点とBoole則および
Legendre3分点のグループ、台形則を示す。
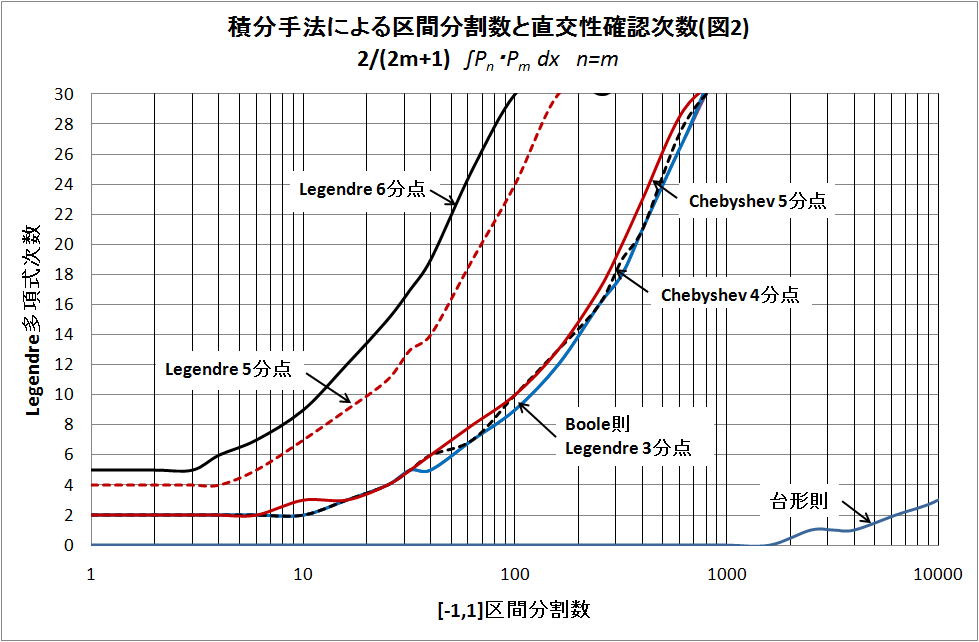
2-2、非対角要素(コード L-2)
この積分は、Pnと両隣の次数Pm=n+1、Pm=n-1の組合せの積分計算は、ゼロと見なしうる値(例えば
1.0e-14程度)であるが、しかし、m=n+2、m=n-2では、ゼロとは言い難い値の時がある。
2-3、計算コード L-2の説明
[-1,1]を等分割して、その等分割した区間に対して、台形則やGauss-Legendre積分を適用する。その計算
結果を分割"数"毎に、csv 形式の file に記入するようにした。このようにある条件で、区別された計算結果
を、その条件毎のファイルにする事は、データの整理を行う事にもなる。また、フォルダを生成し、
その中に、類似条件の計算結果を格納する事も、計算結果の評価の前段階でもある。これらは、第 0 章の
フォルダ生成にも示している。
以下にコードと説明を示す。なお、記載のコードでは、数値積分の部分は、次章にも記載するので、
一部省略して記載する。
コードの抜粋
vector<int>div0(26,0);//計算する分割数
div[0]=1;
・・・
div0[25]=25000;
・・・
for(int i=0;i<div0.size();i++)
{
//分割"数"毎にcsv形式のfile出力を行う準備
stringstream division;
division <<div0[i];
string str = division.str();
char dirdata1[BUFFSIZE];
_getcwd(dirdata1,BUFFSIZE);// <direct.h>が必要
string file_end="div_LegendrePXX_YY.csv";
string file_name="\\"+str+file_end;
strcat_s(dirdata1,file_name.c_str());//file名のdirを生成
fstream out001(dirdata1,ios::out | ios::binary |ios::app);
説明
a、分割数 下記 div0[i] は文字列ではなく、数値である。
vector<int>div0(26,0);
b、これ div0[i] を一旦 stringstream で文字列として、代入する。
stringstream division; // ヘッダー <sstream> が必要
division <<div0[i];
c、文字列の操作が容易なstring 型に .str() で変更。
string str = division.str();
d、コードの置かれたディクトリ情報を _getcwd で dirdata1 に得る。
char dirdata1[BUFFSIZE];
_getcwd(dirdata1,BUFFSIZE);
e、file名に、分割数を取り込んだstring型のstrを付け加える。
file名とし、データの後処理が行い易いように、拡張子部分を「 .csv 」とする。
また、ディクトリを構成できるように \\ を先頭に付ける。
string file_end="div_LegendrePXX_YY.csv";
string file_name="\\"+str+file_end;
f、上記の file_nameは、string型で終端にNULL文字がないので、終端にNULL文字のあるchar型に
c_str() で変更。
file_name.c_str()
g、上記 dirdata1 と file_name.c_str() をchar型の文字結合 strcat_sで、
分割数を含んだ新たなディクトリを生成する。
strcat_s(dirdata1,file_name.c_str());
h,この新 dirdata1 をファイル名として、fstream に代入。
fstream out001(dirdata1,ios::out|ios::binary|ios::app);
上記 a~h は、c++ フォルダ生成にも示している。
対角要素、非対角要素の直交性計算を同時に行う。Legendre多項式のそれぞれの次数の係数を一つの
vector<double>hxに代入する。hx[i] から取り出し算出。
Chebyshev多項式
1、Chebyshev多項式この多項式には、T(x)とU(x)の2つが主である。第一種T(x)を35次まで算出し、m=nとm≠nの直交性を
Gauss-Legendre、Chebyshev、Newton-Cotes法で確認した。
・Chebyshev多項式の Tn(x) の各次数毎での各係数 (コード C-1 )
35次までの各係数の算出方法は、漸化式により逐次算出した。これらの係数を コード C-1 に示す。
漸化式は、下式 2-(1) 式に示すように、三項で示され、2項目に x を含む。
また、0 次の T0(x) は、2-(2) 式で、1 次の T1(x) は、2-(3) 式で示される。
上記の二つの式から、漸化式 2-(1) 式から、2 次の T2(x) を2-(4) 式のように、得る事が出来る。
このように逐次に、算出して、得た Chebyshev 多項式の係数を コード C-1 に示している。
なお、このような逐次的な計算によらず、Chebyshev 多項式の係数を再帰的に得る事が出来るという事が
記述されているので、再帰的な手法で得られた高次の Chebyshev 多項式の係数比較を行う事を推奨したい。
2、直交性の数値的検証
直交性の確認計算では、重み 1/√(1-x^2)を持ち、 x=cosθ とした。この x=cosθ の変換は、web上で公開
されている川上一郎著の"数値計算の基礎"の P.219 の 5.6.3 節 "特異関数の数値積分"にも拠っている。
Chebyshev 多項式の直交性を算出する式は、上述のように重み係数を持ち 2-(5) 式で示される。
上記の 2-(5) 式に、上述に従い、以下の変数変換を施す。
この変換で、積分域 [ -1,1 ] が [ π,0 ] ( π:パイ) になる。
この変換で、両辺の微分を行うと、下式となる。右辺に注目するとマイナスの係数が存在する。
このマイナスの係数は、積分域を [ π,0 ] を [ 0,π ] に変更できる事を意味し、以下の式が成り立つ。
上記の 2-(8) 式と 2-(9) 式を数値計算により、確認した結果を以下に示す。
2-1、対角要素 (コード C-2)
対角要素の直交性を数値計算で確認した。これの計算は、上述の通りである。正規化(1.0)するために、
π/2 (π;パイ)で、割った。分割数の増加と伴に、 1.0 に至った対角要素の次数を、Newton-Cotes法、
Gauss-Legendre法、Gauss-Chebyshev法 毎に下図にまとめる。64 bit の制約が生じている。
・Newton-Cotes法
均等100分割程度で、Chebyshev多項式の30次までの直交性を確認できる。100分割以上からは、徐々に
次数が上がる。この傾向は、それぞれの手法(Cotes法、Legendre法、Chebyshev法)で同じである。
背景には、変数変換の cos の計算精度が大きな因子ではないかと考える。
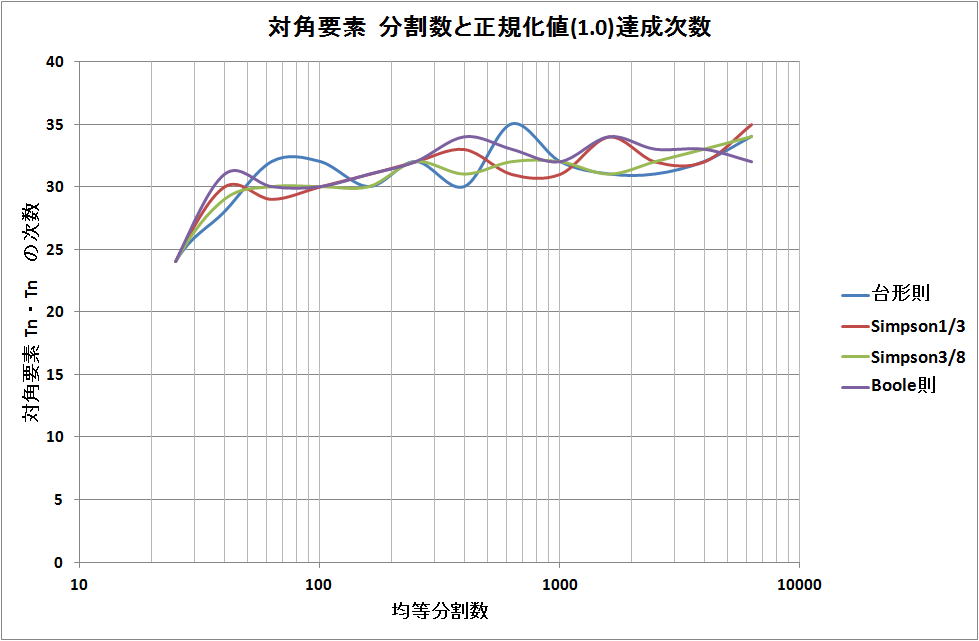
・Gauss-Legendre法
均等100分割程度で、Chebyshev多項式の30次までの直交性を確認できる。
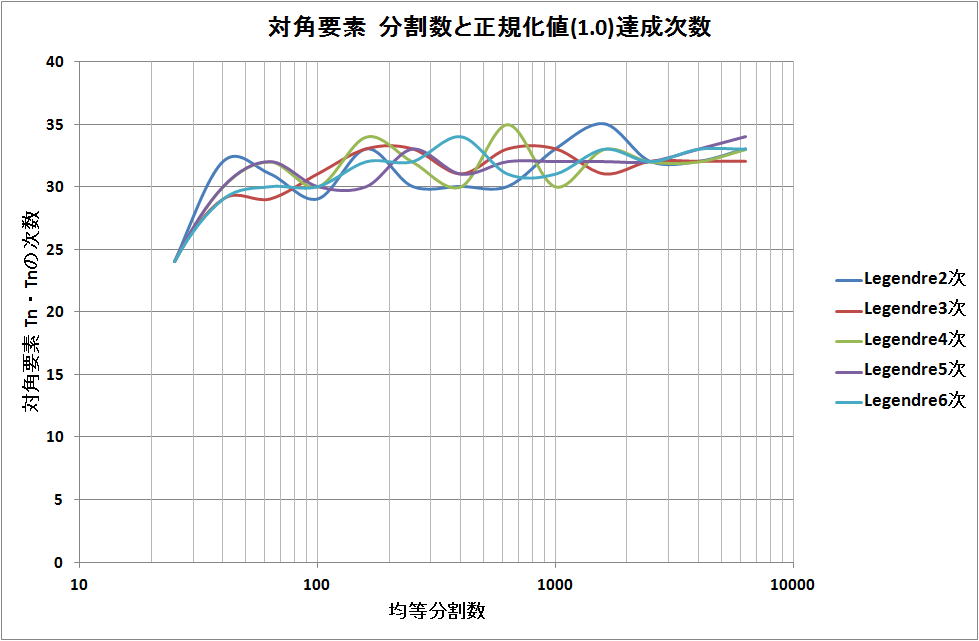
・Gauss-Chebyshev法
均等100分割程度で、Chebyshev多項式の30次までの直交性を確認できる。
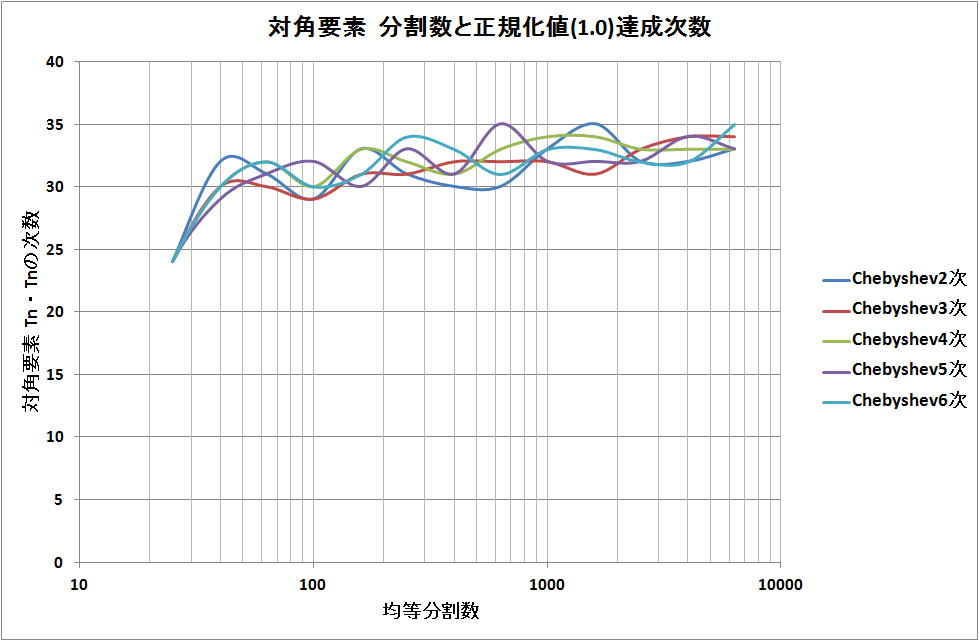
2-2、非対角要素 (コード C-2)
直交性の確認のためには、非対角要素の積分値もゼロになる事の確認を行う事も必要である。
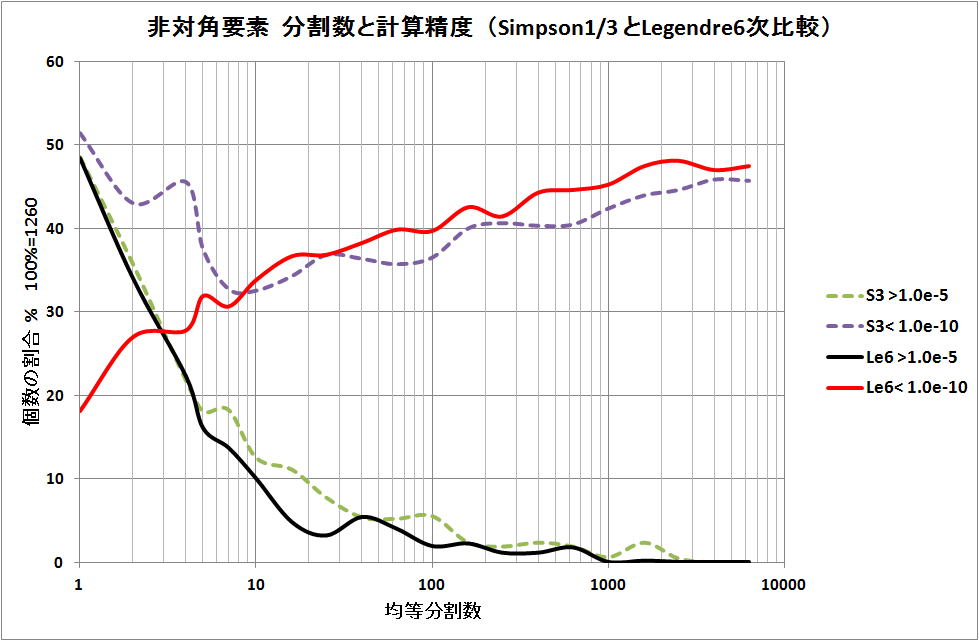
下図に、数値積分 Newton-Cotes 法の一つ Simpson 1/3則と 重み付積分 Legendre 法の 6次積分法での
非対角要素(n≠m、n,m は Chebyshev多項式 Tn(x) の次数)の [0,π] 区間の分割数と計算精度の変化を示す。
Simpson 1/3則と Legendre 6次の手法も、分割数を増加させると、非対角要素の積分値の1.0e-5よりも
大きなケースは、割合(全体計算数 1260 ケ-ス)が低減する。Simpson1/3則の場合、分割数 4000 以上で、
Legendre6次の場合、分割数 1000 以上で、その割合がゼロになる。
また、両者とも、積分値が 1.0e-10 以下となるケースは、分割数増加で、その割合が増えてくる。6300 分
割数では 45% 以上となる。この事は、1.0e-5 から 1.0e-10 の範囲にあるケースは、6300分割でも約 55%
もある事になる。しかし、分割数が更に大きくなると、この 55% が低減する事は予想される。
2-3、計算コード C-2 の説明
Chebyshev 多項式の直交性確認計算は、上記 1 節の Legendre 多項式の直交性計算を基に、
修正を施し、行った。
主な修正個所を Legebdre 多項式の直交性確認計算との比較で示す。
1)積分域
・Legendre 多項式の場合
double x0=-1.0;
double x1=1.0;
・Chebyshev 多項式の場合は、cosに変数変換を行い、一般に θ0 , θ1 と書く所を x0 、 x1 とした。
double x0=0.0;
double x1=PI;
2)変数の計算
・Legendre 多項式の場合
for(int i=0;i<m+1;i++)
{
p_xn0[i]=pow(x0+j*h,i);
p_xn2[i]=pow(x0+j*h+h/4.0,i);
p_xn3[i]=pow(x0+j*h+h/3.0,i);
p_xnm[i]=pow(x0+j*h+h/2.0,i);
p_xn6[i]=pow(x0+j*h+2.0*h/3.0,i);
p_xn7[i]=pow(x0+j*h+3.0*h/4.0,i);
p_xn1[i]=pow(x0+j*h+h,i);
}
・Chebyshev 多項式の場合は、x=cosθ に変換しているので、変数θ(x0等)を cos で算出すれば良い。
for(int i=0;i<m+1;i++)
{
p_xn0[i]=pow(cos(x0+j*h),i);
p_xn2[i]=pow(cos(x0+j*h+h/4.0),i);
p_xn3[i]=pow(cos(x0+j*h+h/3.0),i);
p_xnm[i]=pow(cos(x0+j*h+h/2.0),i);
p_xn6[i]=pow(cos(x0+j*h+2.0*h/3.0),i);
p_xn7[i]=pow(cos(x0+j*h+3.0*h/4.0),i);
p_xn1[i]=pow(cos(x0+j*h+h),i);
}
3)解析解
・Legendre 多項式の場合
double ana=1.0;//anaは解析値を示す。(解析値 ana で割算を行うので 1.0 を初期値とする)
if( k==L) ana=2.0/(2.0*L+1);
・Chebyshev 多項式の場合
double ana=1.0;//anaは解析値を示す。(解析値 ana で割算を行うので 1.0 を初期値とする)
if( k==L) ana=PI/2.0;
if( k==0&&L==0) ana=PI;
4)その他
Function文の名称が異なる。多項式の次数が異なる。
3、使用したSTLおよび関数
vector()、xxx.push_back()、xxx.resize(xxx.size())、inner_product()、multiplies()
Bessel関数
1、Bessel関数の概要Bessel関数は、電荷のポテンシャル分布、電磁波の円筒状の出口の状態、太鼓の膜の状態や熱伝導の状態の解
明の時に必要となる関数である。以下に J0(x) と J1(x) の適用例を示す。
1) J0(x) の適用例
ポテンシャル分布は、電磁気学の教科書にあるように、Laplace方程式を円筒座標 r , φ ,z を用い、以下のよう
に表し、
更に、
のように変数分離する。変数分離後の円筒座標の方程式は、以下の三つの方程式となる。
上記の R に関する微分方程式 B-3式で、r を x とし、その解は、Bessel関数であるので、Jn(x) とすると、以下
の式となる。
ポテンシャル分布は、
円筒状のポテンシャル分布は、以下の式で示される。
2) J1(x) の適用例
電磁波の円筒の出口 ( 半径 a )の伝送の電力の透過係数 T は、以下の式で示される。
3)円膜や熱伝導について
円膜については、直交関数の本に、図がある。熱伝導については、多くの偏微分方程式の教科書に記載が
あるので、割愛する。
2、Bessel関数の特性
この関数の特性については、スミルノフ高等数学教程や数学の本に詳しく記載されているので、詳細は記載
しない。
不等間隔の数値積分の検証計算として、この関数の特性を使用するので、以下に示す。
(この関数の直交性を、数値計算で確認する事は、現時点では行わない。考えが進んでいない。)
2-1)Bessel関数の解の級数表示(スミルノフ高等数学教程より)
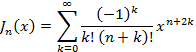 B-9式
B-9式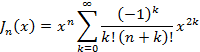 B-10式
B-10式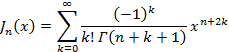 B-11式
B-11式ただし
2-2) フーリエ表示の解
n が分数時も含めた場合は以下となる。整数時は、第一項のみでよい。(スミルノフの教程より)
2-3)Besel関数の関数間の関係
2-4)Bessel関数のグラフ表示 (コード B-1)
以下に Jn(x) の特性を図示する。
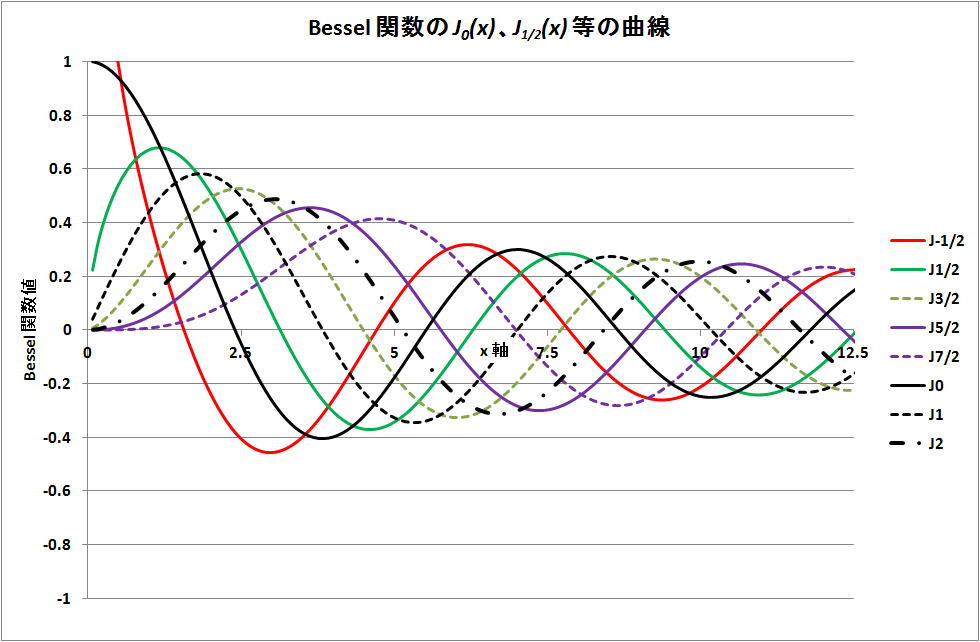
・本図作成のための J0(x) 、J1(x) 、J2(x) のコードに関する説明
再帰法で、 n! 等を求める事が出来る。気が変わり、実際の数式で求めた。
3、Bessel関数間の微分と積分の関係
3-1)微分と積分の関係
Bessel関数の微分の B-14 式と B-15 式に着目すると、両者の和は、下記の B-16式となる。
上記の両辺を定積分すると、微分の J'n(x) は Jn(x) となり、左辺は通常のBessel関数の定積分で、以下
の式となる。
すなわち、整数の Jn(x) については、以下となる。
また、分数の J(2n+1)/2(x) についても、以下の式が成立すると考えられる。この関係の成否は両辺の計算が
合致すれば、成立する事にもなる。
3-2)関数の微分と積分の具体的な関係
上記の B-18式、B-20式で、次数 n を具体的に示すと、以下の式となる。
・Bessel 0 次の微分(この式は、B-15式の n=0 の時で、また、B-18式とB-13式の関係からも成り立つ)
・Bessel 1 次の微分
・Bessl 1/2 次の微分
・Bessel 3/2 次の微分
・Bessel 5/2 次の微分
4、不等間隔の数値積分(コード B-2)
Bessel関数間の微分と積分の関係を利用し、案出した不等間隔の数値積分の計算式の検証を行った。
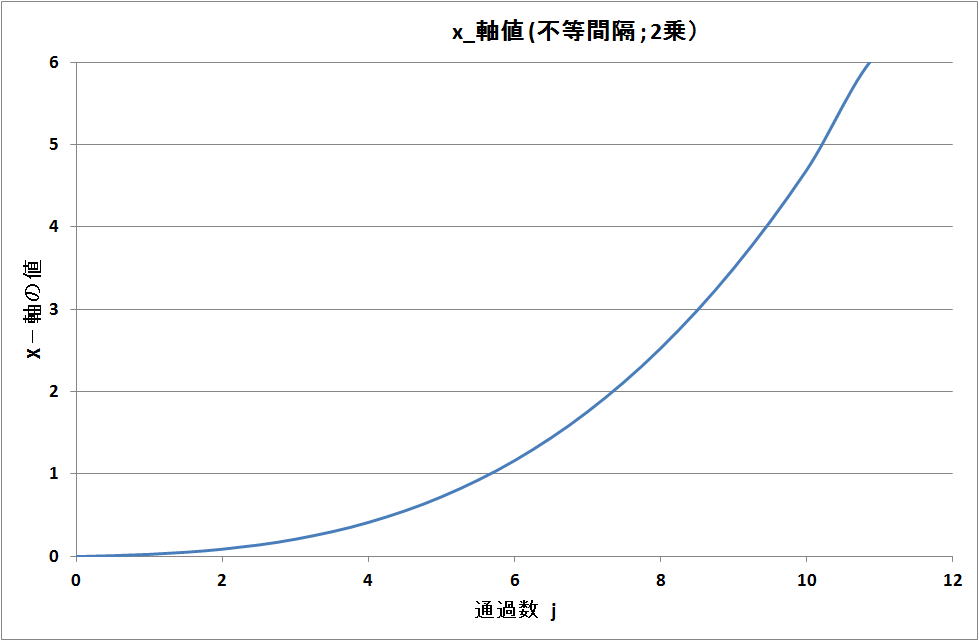
4-1)x 軸の不等間隔のデータ作成
不等間隔が、二乗のピッチで進むように計画した。これを下記のコードに示す。
j*j の個所が二乗のピッチで進む作用を行う。なお、線形の不等間隔の場合は"数値計算 第 7 章"に記載。
double p=0;また、上記の計算結果を横軸を j 、縦軸を x_axis[j] の時で、下図に示す。二乗の曲線である。
int kdiv=400;
int m=0;
double x=0.0;
vector<double>x_axis(kdiv+1,0.0);
for(int j=0;j<=kdiv;j++)
{
p=0.75*(double)j*j+p;
x_axis[j]=2.0*PI/kdiv*(p+j);
if(x_axis[j]>2.0*PI) { m=j; break;}
}
x_axis[m]=2.0*PI;
x_axis.resize(m+1);
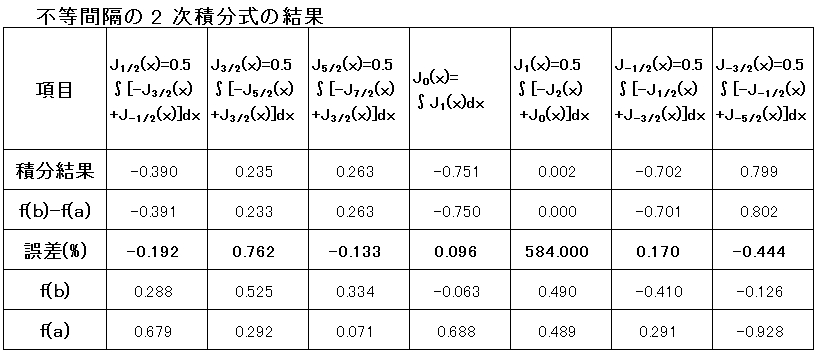
4-2)不等間隔の数値積分結果
B-18式、B-20式による、B-22式、B-24式等の積分計算を二次積分式、三次積分式、四次積分式、
五次積分式に基づき、不等間隔で行った結果を表にして示す。
表の項目の"積分結果"は、B-18式、B-20式の右辺の計算結果である。
" f(b) - f(a) " は、左辺の結果である。"誤差" は、(右辺 - 左辺)/左辺のパーセント表示である。
・二次積分式の結果
誤差は、1 % 以下であるが、J1(x) すなわち、B-24式の誤差は高い。要因の検討は後日行う。
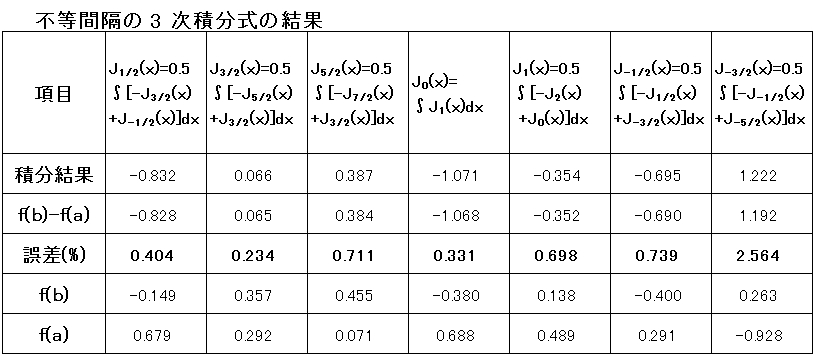
・三次積分式の結果
J-3/2(x) を除けば、誤差は 1 % 以下である。
・四次積分式の結果
J3/2(x) と J-3/2(x) を除けば、1 % 以下である。
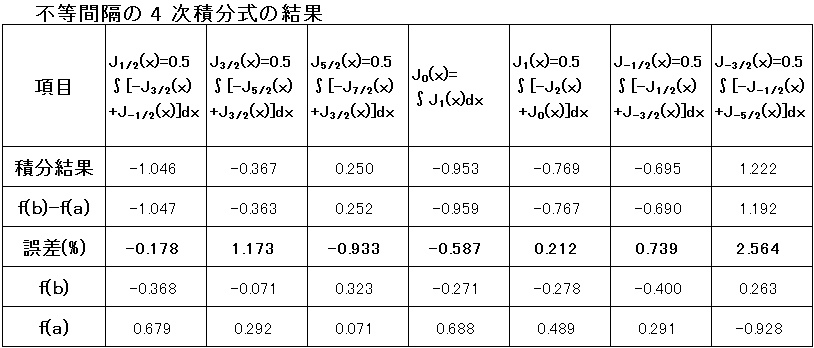
・五次積分式の結果
殆ど、 1 % 以上の誤差である。
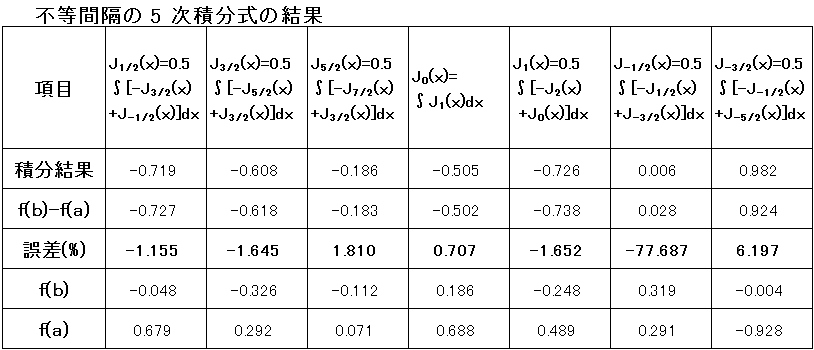
・更に、次数の高い積分式の計算が必要である。
・不等間隔のデータで、ここでの計算のように2乗的不等間隔ではなく、線形的に不等間隔の時は、計算誤差
が、ここで示した二乗的な場合より、小さいという結果を得ている。
5、Bessel関数の分数次の具体的な数式
以下の式で、7/2 次 J7/2(x) は著者が計算したもので、それ以外は、スミルノフ高等数学教程に拠った。
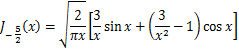 B-29式
B-29式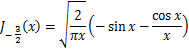 B-30式
B-30式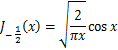 B-31式
B-31式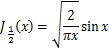 B-32式
B-32式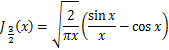 B-33式
B-33式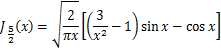 B-34式
B-34式 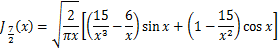 B-35式
B-35式6、参考図書
・ポテンシャル分布の説明
パノフスキー・フィリプス著(訳 林忠四郎 他)"電磁気学”第2版 P.103 吉岡書店(1970)
・透過係数の説明
John David Jackson 著 "Clasical Electrodynamics" P.295, John Wiley & Sons, Inc. (1962)
・円膜の図
伏見康治 他 著 "直交関数系" P.135 図6.3, 共立出版(株)(1987年)
及川正行 著 "偏微分方程式" P.206 図8-1, (株)岩波書店 (1997年)
・数式について
"スミルノフ高等数学教程" Ⅱ巻 第一分冊 P.131 ,Ⅲ巻 第二分冊 P.476, 共立出版(株)(昭和45年 20刷)
7、感想
Bessel 関数は、多くの技術分野で広く使われていると思われる関数である。扱いが難しい。J3(x)の計算を行
ったが、収束しない。x^3を外に出し、残りの項で、計算を行ったが、それでも、収束しない。更に、特定の
項から、また x^3 を外に出し、計算を行うとしたが、中止した。時間をこれ以上割く事に疑問を持ったため。
直交関数系は、三角関数の遺伝子があるので、フーリエ展開から求める事ができるのではないかと思い。
多項式級数展開(Legndre、Chebychev)
1、Legendre 多項式による級数展開1-1、Legendre 多項式による級数展開の係数の導出
被関数 g(x) が、[-1,1] 区間で定義されていて fn(x) (n=0,1,...) の多項式に展開できるとする。残余の不記載。
この展開可能な多項式を Legendre 多項式 P0、P1、・・・Pn とすると、以下になる。
上記の式に Legendre 多項式の 0 次の P0 を掛けて、区間 [-1,1] で積分する。
1-(3)式
Legendre 多項式は、P0・P0 の項以外、Legendre多項式の節の 1-(5) 式に示すように 0 となるので、
従い、以下となる。
1-(2)式に Legendre 多項式の 1 次の P1 を掛けて、区間 [-1,1] で積分する。
1-(6)式
1-(6) 式は、P1・P1 の項以外、Legendre多項式の節の 1-(5) 式に示すように 0 となる。
同じく、以下の式となる。
1-(2)式にLegendre多項式の n 次の Pn を掛けて、区間[-1,1]で積分する。
1-(9)式
1-(9)式は、Pn・Pn の項以外、Legendre多項式の節の1-(5)式より 0 となり、1-(10) 式を得る。
結論として、1-(2) 式中の係数 an は、1-(11) 式となる。
2、Legendre多項式の級数展開の適用計算(連続関数への適用 等・不等間隔分割)
上記の 1-(11) 式を基にした級数展開を 2 つの関数で計算した。この Legendre 多項式による級数展開は、
被関数が多項式の場合に有用であるという見解を読んだ。このために Chebyshev 多項式の 11 次と関数、
sin(πx) に対し、級数展開を図った。また、Bessel 関数にも、級数展開を試みた。
なお、不等間隔の離散データの級数展開については、次次章の数値計算 7 で計算する。
更に、係数 an の算出計算は、以下の条件で行った。
・定積分 1-(11) 式の数値積分手法: ( 数値計算 6 と同じ)
台形則とSimpsonの1/3則、3/8則、Boole則、
重み付積分 Legnedre 2次、3次、4次、5次、6次、Chebyshev 2次、3次、4次、5次、6次の方法
・[-1.0,1.0] 区間の均等分割数: 1 から 10000
・算出した係数 an の検証計算:得た an で、 [-3,3] 区間において比較
( Legendre 多項式級数による再構成多項式と原関数との比較)
a) 11 次の Chebyshev 多項式への適用 (コード D-1)
・Legendre多項式の級数展開を 12 次まで (被対象関数 11 次に 1 次分追加)
a.1) コード D-1 の説明
Legendre 多項式の 34 次までの各係数は、Legendre 多項式 1 に示している通りである。また、具体的な
計算は、Legendre 多項式の直交性確認計算 2 とほぼ同じである。被対象関数は gx として計算した。
更に、コード作成を容易にするために、Legendre 直交性確認計算(コード L-2 )を利用し、Legendre 多
項式の次数の低減のの繰り返し部 fx の終了後に、 an 係数を求めるようにした。
この an 係数で、再構成による検証計算を行った。
付け加えるに、下表の係数の値は、ある意味ではいつも同じ数値である。上記の各数値積分手法は、公知
で確立されている。被対象の関数や級数展開の関数も同様である。従い、計算の検証になる数値である。
a.2) 係数 an の検証
1-(11) 式の g(x) の x の最大次数は 11 である。11 次の Chebyshev 多項式の t11[11]=1024 である。
また、Legendre 多項式の 11 次は、p11[11]=88179/256 である。Pnの級数展開で、 11 次以上は明らか
に存在しないので、両者の比較から an の値を求める事が出来る。従い、コードが正しければ、
an=t11[11]/p11[11]=1024・256/88179=2.972862 2-(1)式
となるはずである。(2・11+1)/2は、正規化のための定数故に、この場合は不要である。
a.3) 級数展開時の係数
等分割 10000 時の級数展開の各次数での係数を下表に示す。
12 次は、略ゼロである。
11 次の係数は、下表の p_11 に示すように 2.972862 で上記の計算値と同じである。従い、問題ないコー
ドである。
a.4) 級数展開式
11 次の Chebyshev 多項式の偶数次は 0 であるので、an の偶数次は、略ゼロである。
Chebyshev t11 は、以下のように級数展開できる。(以下の値は Legendre 6 分点時)
t11= 2.792862・p11 + 0・p10 - 1.412・p9 + 0・p8 - 0.325・p7 + 0・p6 - 0.142・p5 + 0・p4
- 0.068・p3 + 0・p2 - 0.026・p1 + 0・p0
2-(2)式
a.5) 計算結果の表
a.6) 級数展開の再構成
級数展開再構成の計算結果(分割数10000のLegendre6分点法の係数 an の2-(2)式)と原関数を下図に示す。
両者の差は [-3,3] 区間は 10の-4乗以下で一致し、明示出来ないが、[-1,1] では、10の-12乗以下である。
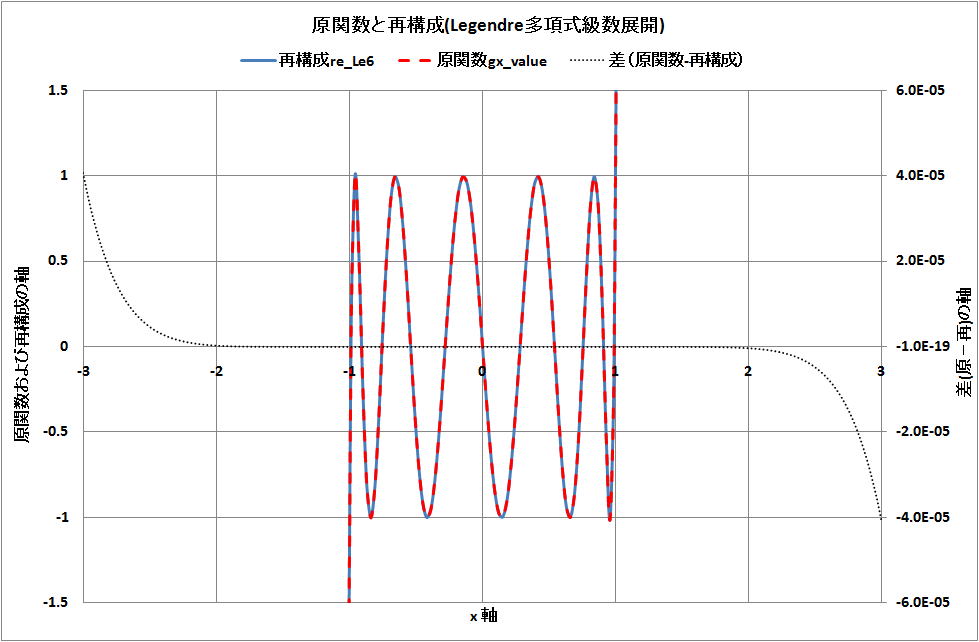
すなわち、t11 は [-1,1] の範囲で以下となる。
t11= 2.792862・p11 - 1.412・p9 - 0.325・p7 - 0.142・p5 - 0.068・p3 - 0.026・p1
2-(3) 式
a.7) 直交関数 Legendre関数による一次結合
t11 の関数は、Legendre 関数の一次結合である事を 2-(3) 式は意味するので、この意味(一次結合の
意味)を図でしめす。 一次結合と線形結合は同じ事であるとして、記載している。
・Legendre 関数(多項式)の 11 次式 p11 の場合
原関数 (t11) と全く異なる。
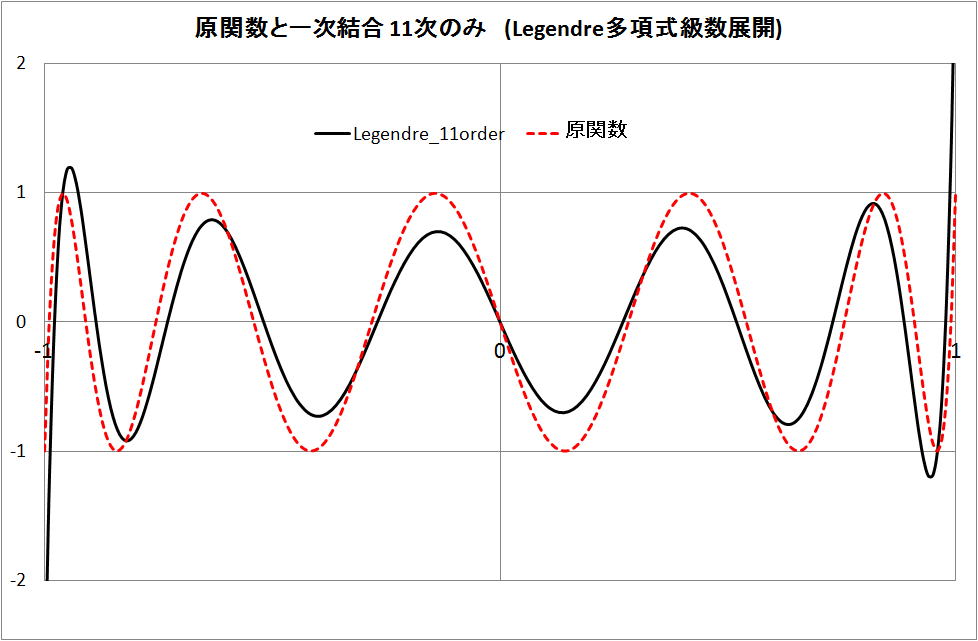
・Legendre 関数(多項式)の 11 + 9 次式 p11 +p9 の場合
原関数 (t11) に少し似てきているが、異なる。
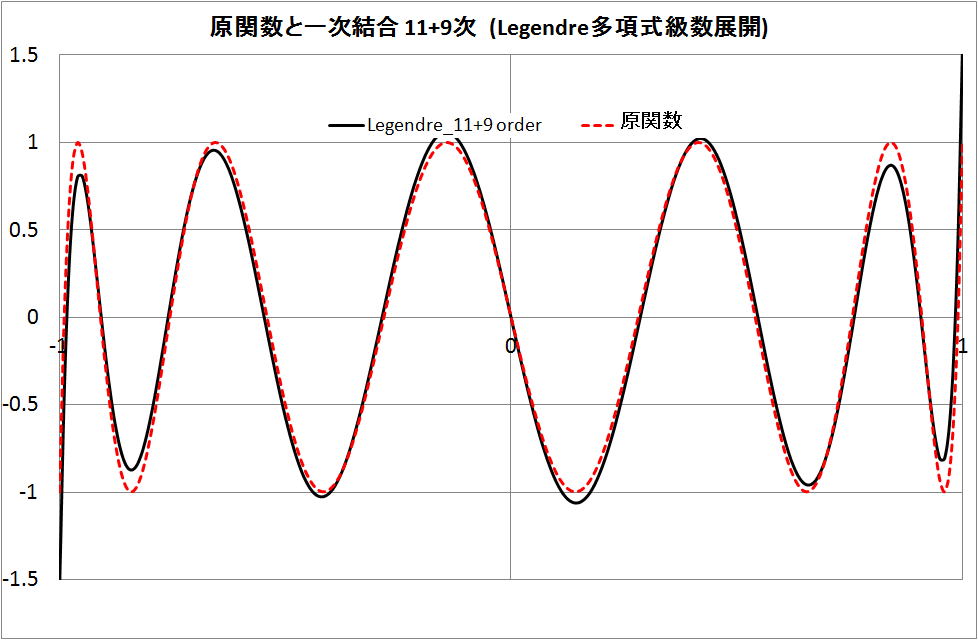
・Legendre 関数(多項式)の 11 + 9 + 7 次式 p11 + p9 + p7 の場合
原関数 (t11) と類似であるが、x 軸の -1 と +1 で誤差がある。
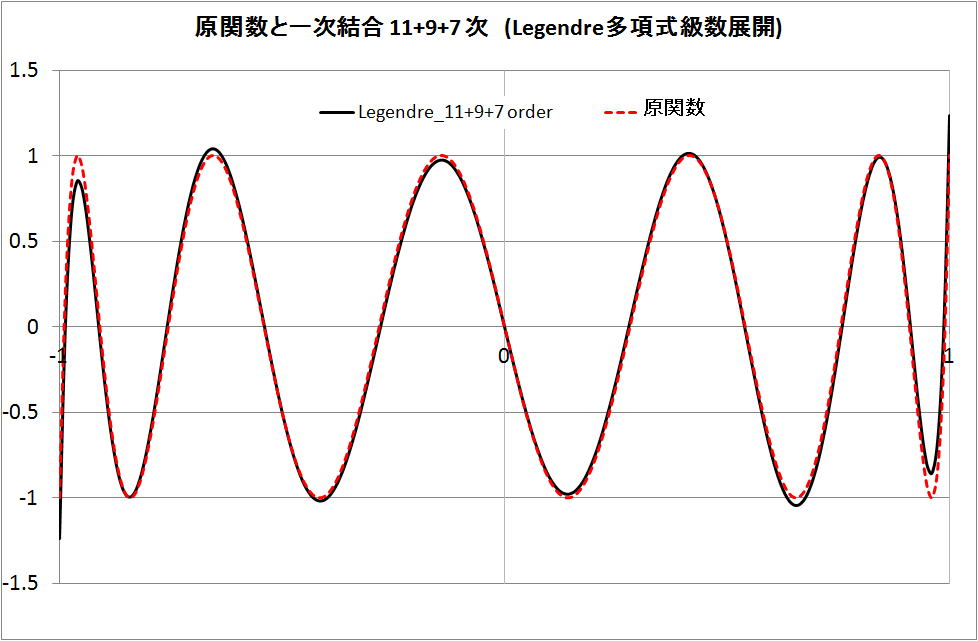
・Legendre 関数(多項式)の 11 + 9 + 7 + 5 次式 p11 + p9 + p7 + p5 の場合
原関数 (t11) と類似であるが、x 軸の -1 と +1 で、まだ、誤差がある。
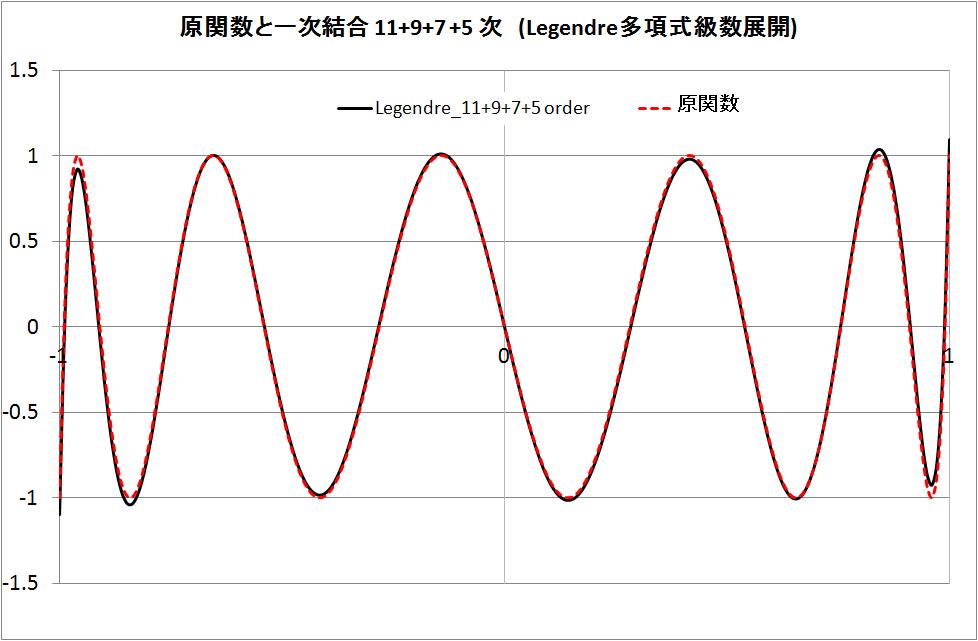
・Legendre 関数(多項式)の 11 + 9 + 7 + 5 + 3 次式 p11 + p9 + p7 + p5 + p3 の場合
原関数 (t11) とほぼ同じである。x 軸の -1 と +1 での差は見えない。実用上支障はないのでは。
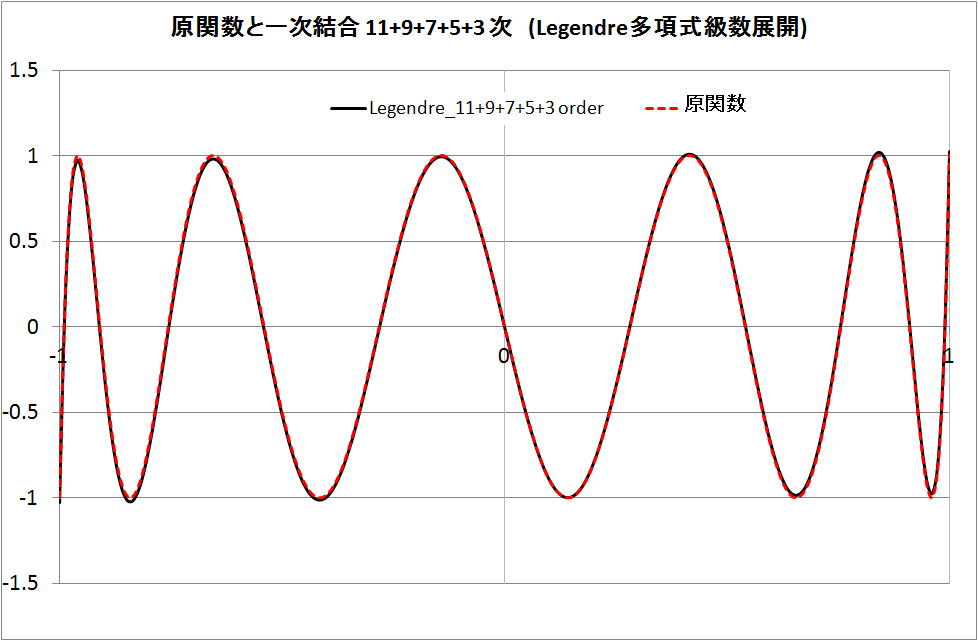
・Legendre 関数(多項式)の 11 + 9 + 7 + 5 + 3 + 1 次式 p11 + p9 + p7 + p5 + p3 + p1 の場合
原関数 (t11) と同じとなる。
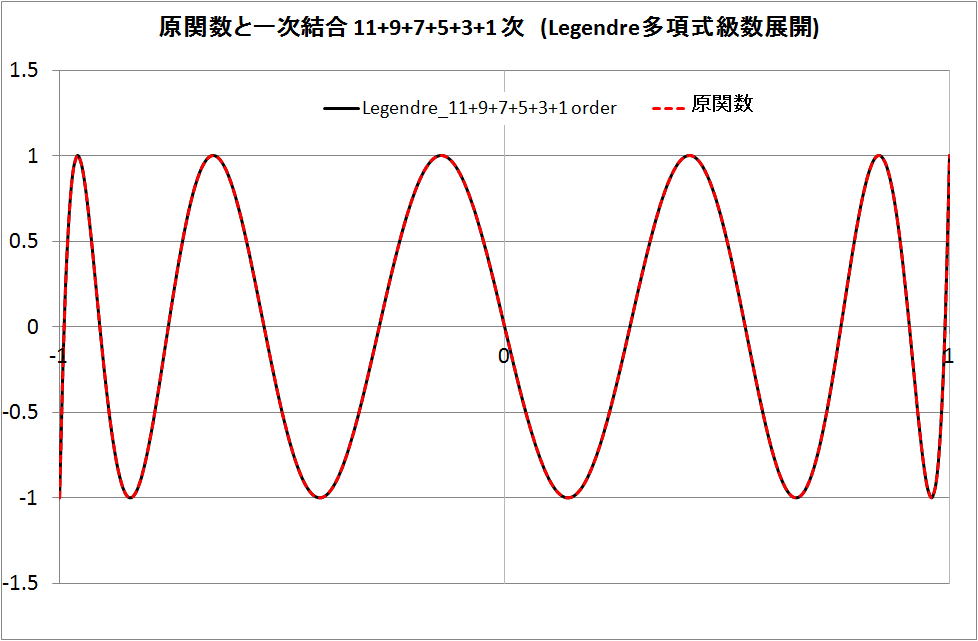
ある関数を直交関数の一次結合で示す事が出来るという事は、複雑な関数を実用上支障のない範囲で
低次の式あるいは高次の式を除外する事で近似できる事を意味する。
b)、通常関数 sin(πx) への適用 (近似式) (コード D-2)
・Legendre 多項式の級数展開を通常関数 sin(πx) に 23 次まで適用した。 sin(πx) を 23 次まで近似した。
級数の an の係数算出 : [-1,1]
再構成との比較 : [-3,3]
・コード D-2 の説明
全体のコードの内容は、上記のコード D-1 とほぼ同じであるが、被対象関数の記述法を変えた。
被対象関数は function 文の g_function(x,a,b) 内に sin(πx) を記述した。この g_function(x,a,b) で 予備
のパラメータ a,b は共に 0.0 である。
・等分割数 10000 でのLegendre多項式の級数展開の an の係数を下の表に示す。
また、Legendre6分点法では、以下の級数展開となる。 sin(πx) (π:パイ)が奇関数である事を考慮した。
sin(πx) = - 0.0・p23 - 0・p22 + 0.0・p21 + 0・p20 - 0.0・p19 + 0・p18 + 3.8999e-11・p17
- 0・p16 - 3.9839e-09・p15 - 0・p14 + 3.0952e-7・p13 + 0・p12 - 1.75369e-05・p11
- 0・p10 - 0.00068221・p9 + 0・p8 - 0.0166423・p7 - 0・p6 - 0.21928955・p5 + 0・p4
- 1.1582419・p3 - 0・p2 + 0.95492966・p1 + 0・p0
2-(3)式
上式で、展開次数 p17 以下の係数 an が有効 と考えられる。その理由は、各数値積分手法で、ほぼ同じ値
を得ているからである。long double が double より大きくなると有効な展開の次数は高くなると考える。
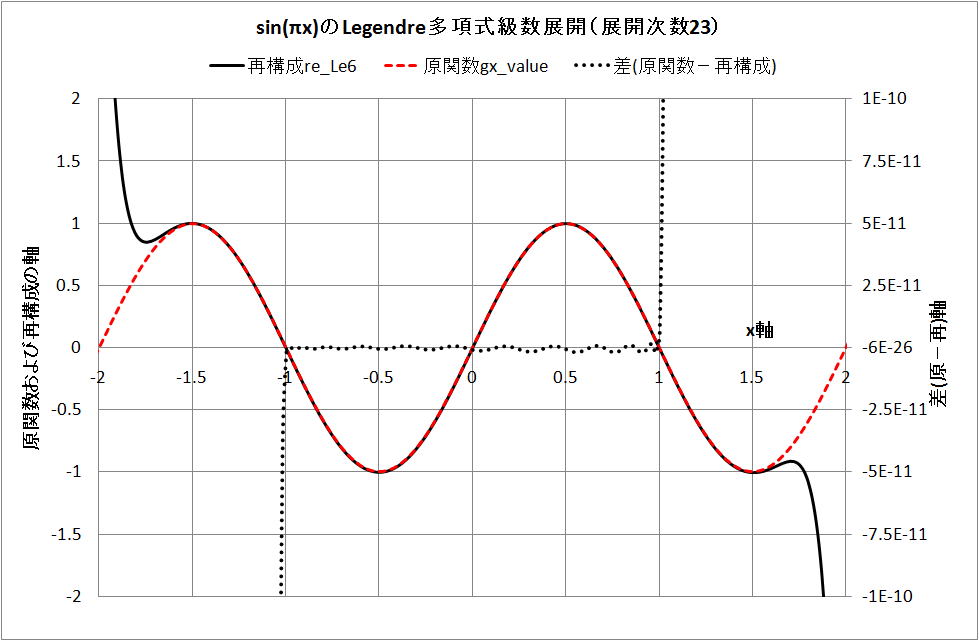
・級数展開の再構成による計算結果(等分割数10000のLegendre6分点法の係数 an )の曲線(上表の p_23 から
p_0 の係数を用いたもの。2-(3)式ではない。)と原関数の曲線を下図に示す。計算は、[-3,3] で行ったが、
下図では [-2,2] の範囲を示している。
[-1,1] 区間内はよく一致している。しかし、区間外は離れるに従い乖離が大きくなる。
また、Legendre多項式の 17 次までで、級数展開を行った結果、[-1,1]区間外での乖離の程度が減少した。
17 次以上が誤差になっている事は、 数値の bit 数(浮動小数点の桁数)の制約が強いといえる。
なお、奇関数である sin(πx) を区間を変え、 [0,1] で、Legendre級数展開 ( an を 2・an とする。)を行っ
た時の再構成したデータは、上記と同様な結果であり、下図に示す通りである。
しかし、偶関数である cos(πx) をLegendre級数展開を行った場合は、[-1,1]区間での積分の場合は、再
構成した場合は、期待通りであり、問題ないが、[-0.5,0.5] 区間での積分では原関数と全く異なったデータ
となった。偶関数の場合は、 既に p0 成分があるので、フーリエ級数の場合のような a0 成分の抜け落ちは
無いと考えられる。現在、これの理由はまだわからない。
・Legendre多項式による級数展開は、sin(πx) に適用した時、[-1,1] 区間は展開可能である。このような級
数展開が、多項式にのみ有用という見解は、全てについて、当てはまる訳ではないと考える。
しかし、別の計算上の何かが生じる可能性を示唆しているのだろうか。
c)、ベッセル関数 J1/2 への適用 (コード D-3)
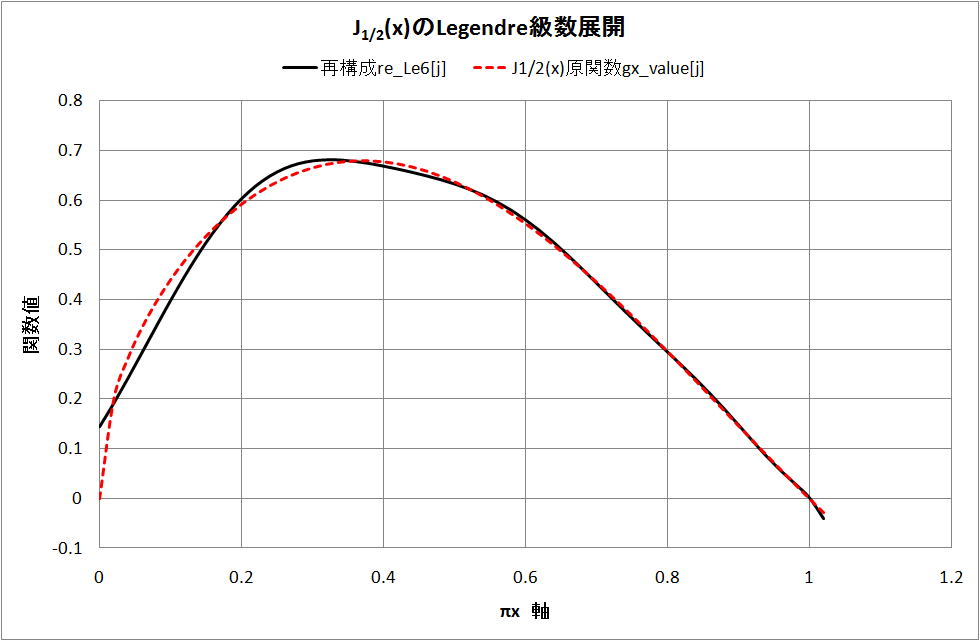
厳密には奇関数ではないが、ベッセル関数 J1/2(πx)=sqrt(2πx/π)・sin(πx)/πx を [0,1] 区間で
Legendre 級数展開( p_29 まで)を行った。 比較結果を下図に示す。
再構成関数は、πx=0.4 までは、差は大きいが、全体として、良く近似している。従い、奇関数のような
関数に対しては、[0,1]での適用は問題ないと考える。
ベッセル関数は、 xの無限級数であるので、次数をもっと高めると近似できる。
参考図書 スミルノフ高等数学教程Ⅲ巻二部 共立出版 昭和45年 訳者代表 福原満洲雄
この図書の第6章 132節 P.450 には、慎重な意見の後に係数 an 算出の結論のみの (49) 式がある。
なお、1-(1)式から 1-(11)式は、上記図書の結論 (49) 式の導出を行うために補足した式である。
3、Chebyshev 多項式による級数展開
3-1、Chebyshev 多項式による級数展開時の係数の算出
この Chebyshev 多項式による級数展開時の係数の算出計算過程は、Legendre 多項式による級数展開時と
同じである。 しかし、係数の値と積分域が異なる。Chebyshev 多項式の場合は、係数は、展開の次数によら
ないが、Legendre 時より計算が少々複雑で、直交計算の時と同じく変数変換を行うので、以下となる。
積分域を [ 0 , π ]、変数を θ とする。
3-2、Chebyshev多項式の級数展開の適用計算(連続関数への適用 Legendre6分点の不等間隔分割)
a)11 次の Legendre 多項式への適用
11次の Legendre 多項式に対して、Chebyshev多項式の級数展開を 11 次まで適用した。
この計算は、2-2、の計算の被対象の関数と級数展開の関数を入れ替えた計算である。
a-1、計算方法について
係数を算出するための積分は、Legendreの6分点法で行った。このLegendreの6分点法は被対象の
関数が Legendre 関数であるから用いたのではなく、精度が高いために使用した。Simpsonの1/3則で
もよい。
a-2、具体的な計算 (コード E-1)
係数算出の計算に変数変換を行い求めているので、この部分を下記に示す。被対象関数とChebyshevnの
級数も、変数 xを cos(θ) に変える事が必要である。
以下で、gx は、被対象の関数 p11 を、fx は Chebyshev 多項式を示す。11次で級数展開を行った。
//an値の格納部分
vector<long double>Le6_an(ak+1,0.0);
for(int L=ak;L>=0;L--)
{
int m=L;
for(int i=L*(L+1)/2;i<m+L*(L+1)/2+1;i++) fx.push_back(hx[i]);
fx.resize(fx.size());
double factor=2.0/PI;//Chebyshevの直交係数の逆数
double h=(x1-x0)/div;
---
---
---
for(int j=0;j<div;j++)
{
// 6分点
double xLe6_0=x0+j*h+h/2.0+h/2.0*x60;
double xLe6_1=x0+j*h+h/2.0+h/2.0*x61;
double xLe6_2=x0+j*h+h/2.0+h/2.0*x62;
double xLe6_3=x0+j*h+h/2.0+h/2.0*x63;
double xLe6_4=x0+j*h+h/2.0+h/2.0*x64;
double xLe6_5=x0+j*h+h/2.0+h/2.0*x65;
for(int i=0;i<m+1;i++)
{
Le6_0=Le6_0+fx[i]*pow(cos(xLe6_0),i);
Le6_1=Le6_1+fx[i]*pow(cos(xLe6_1),i);
Le6_2=Le6_2+fx[i]*pow(cos(xLe6_2),i);
Le6_3=Le6_3+fx[i]*pow(cos(xLe6_3),i);
Le6_4=Le6_4+fx[i]*pow(cos(xLe6_4),i);
Le6_5=Le6_5+fx[i]*pow(cos(xLe6_5),i);
}
for(int i=0;i<n;i++)
{
gLe6_0=gLe6_0+gx[i]*pow(cos(xLe6_0),i);
gLe6_1=gLe6_1+gx[i]*pow(cos(xLe6_1),i);
gLe6_2=gLe6_2+gx[i]*pow(cos(xLe6_2),i);
gLe6_3=gLe6_3+gx[i]*pow(cos(xLe6_3),i);
gLe6_4=gLe6_4+gx[i]*pow(cos(xLe6_4),i);
gLe6_5=gLe6_5+gx[i]*pow(cos(xLe6_5),i);
}
a-3、Chebyshev 多項式による級数展開時の係数
係数は、以下の通りである。偶数次の係数は、ほぼゼロである。Legender の 11 次 p11 が奇関数で
であるので、正しい。Le_6分点積分は Legendre の6分点積分法で、積分を行い、10000分割である。
| Chebyshev 次数 | 係数(Le_6分点積分) | Chebyshev 次数 | 係数(Le_6分点積分) |
| t_11 | 0.336376 | t_10 | 7.08E-16 |
| t_9 | 0.176197 | t_8 | 3.52E-16 |
| t_7 | 0.139103 | t_6 | 3.41E-16 |
| t_5 | 0.122738 | t_4 | -4.24E-17 |
| t_3 | 0.114555 | t_2 | 1.64E-16 |
| t_1 | 0.111031 | t_0 | -8.51E-17 |
従って、p11 は、Chebyshev多項式で、以下のように級数展開できる。
p11 = 0.336376*t11 + 0.176197*t9 + 0.13103*t7 + 0.122738*t5 + 0.114555*t3 + 0.111031*t1
3-(2) 式
a-4、級数展開の再構成と原関数
再構成と原関数の図を下図に示す。最初は、 Chebyshev の 1次 t1 の無い図を、次に全ての次数を含ん
だ図を示す。
・Chebyshev t11 + t9 + t7 + t5 + t3 の図 ( t1 の無い図)
原関数とは合致していない。
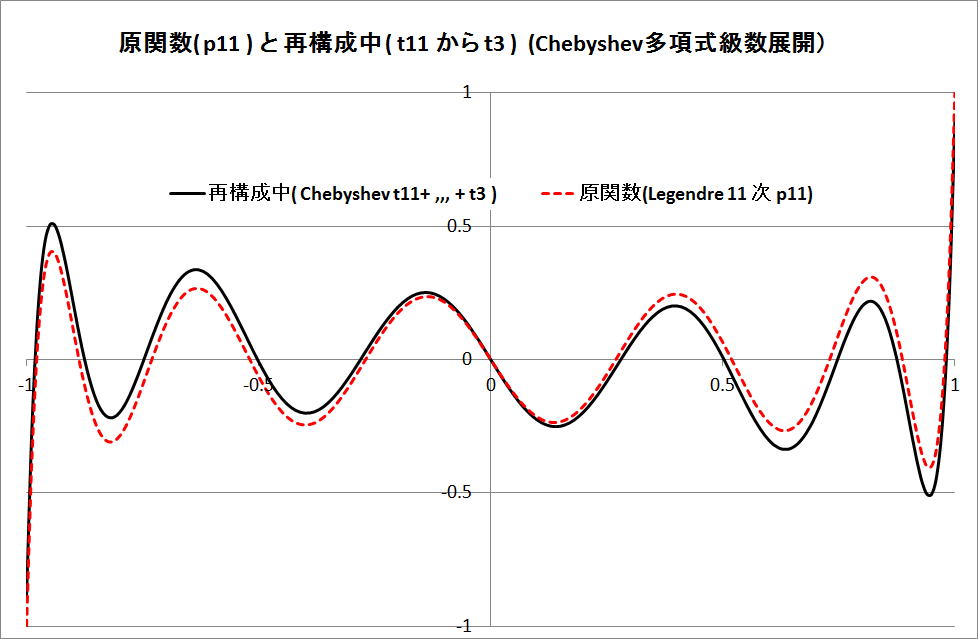
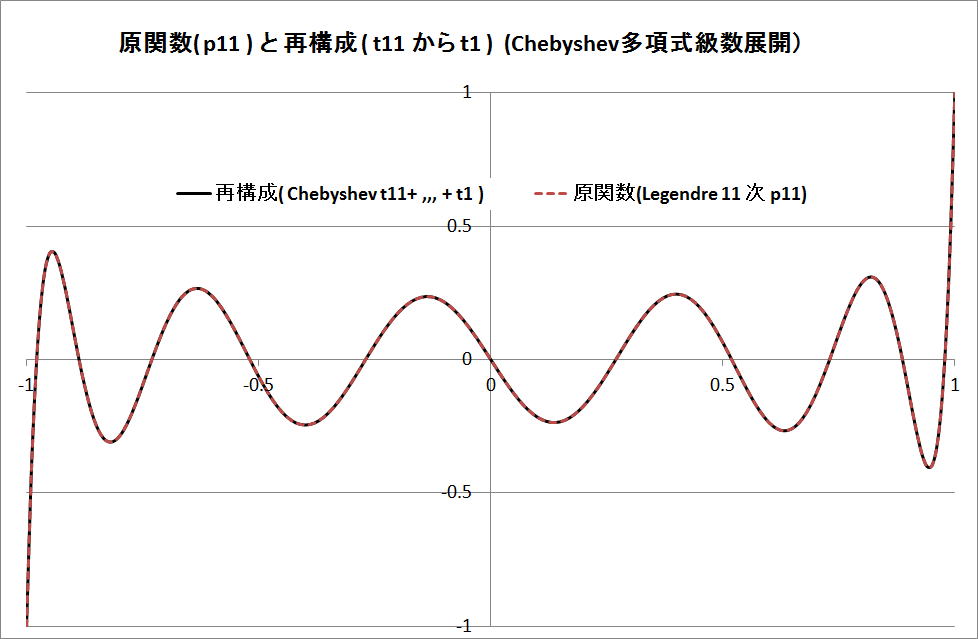
・Chebyshev 級数展開の再構成図 ( t11 + t9 + t7 + t5 + t3 + t1 ) 全てを含む
原関数と合致している。
3-2)sin(πx + π/2 ) ( = cos( πx ) へのChebyshev級数展開
・Chebyshev 多項式での級数展開を関数 sin( πx + π/2 )、すなわち cos( πx )、π;パイ で行った。
級数の an の係数算出域は、[-1,1] で、算出のための積分計算は、 Legendre の6分点で、等分割数は、
10000分割である。
・計算コード の説明
被対象関数は function 文の g_function(x,a,b) 内に sin(πx) を記述した。この g_function(x,a,b) で,
パラメータ a,b を、a=1.0 、 b=π/2 として計算した。
また、cos( πx ) が偶関数であるので、以下の文をコードに付け加えた。
double factor=2.0/PI;//Legendreの直交係数の逆数 正規化
double factorL0=1.0/PI;//Legendreの直交係数の逆数 正規化
---
---
---
Le6_an[L]=Le6_ort*factor;
if(L==0){ Le6_an[L]=Le6_ort*factorL0;}
・計算結果
展開する次数により、再構成と原関数との差が異なる。これを下記にしめす。
なお、 ^-9 は、10^-9 を示し、再構成と原関数との差が 10 の -9 乗である事を意味する。
18 次までの Cheyshev 多項式による級数展開が精度が高い事になる。18 次の再構成の図を下図に示す。
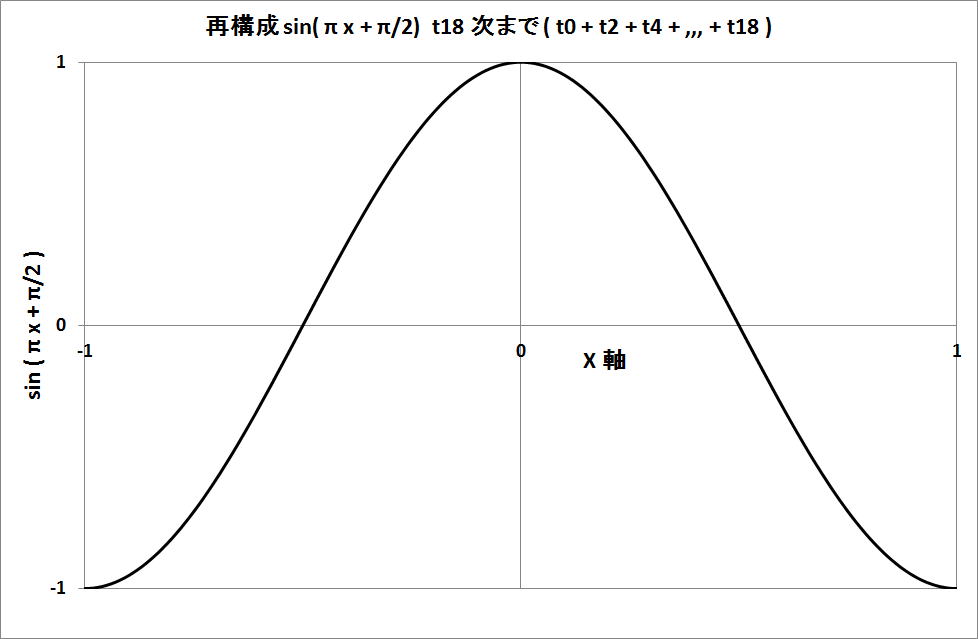
4、多項式級数展開による Maclaurin 展開の係数算出
直交関数である Legendre 多項式や Chebyshev 多項式で、三角関数の sin( πx ) と cos( πx ) を確度高く、
多項式級数展開で近似できる事は、これらの多項式で Taylor 展開、正確には Maclaurin 展開の各次数(x^n) の
係数を近似的に求める事が出来る事を示すので、数値計算で算出する事を行った。
4-1、三角関数の Maclaurin 展開
正弦関数 sin( πx ) の Maclaurin 展開は以下となる。
従い、Maclaurin 展開の係数は、次となる。
また、余弦関数 cos( πx ) の Maclaurin 展開は以下となる。
同様に、Maclaurin 展開の係数は、以下となる。
上記の係数を前述したように、多項式級数展開により算出する。
4-2、具体的な計算 (コード F-1 )
Legendre 多項式と Chebyshev 多項式による級数展開を同時に計算するコードである。
また、計算では、sin( πx ) と cos( πx ) は、x の次数 n の取り方が異なるので、別々に計算した。
コード内では、コメント行として、片側を控えている。
計算の精度比較を行うための係数の真値の算出時には、n! の階乗計算が必要となるので、
この個所の計算は、定石通り、再帰法を用い、関数 long long recursive_call_for_factorial で行った。
級数展開で得た各次数の係数から、次数毎の級数展開の係数の和により、Maclaurin 展開の係数の算出を
行った。この和の算出には、 c++の arry/STL を利用して、一般的な方法で積算の和を行った。この積算和
の計算には、STL のaccumulate を使用出来たのではと思うが、次回とする。
4-3、計算結果
計画通り、Legendre 多項式級数展開、Chebyshev 多項式級数展開の係数から Maclaurin 展開の係数を算
出が可能となった。直交関数を用いれば、積分から微分の微係数算出が可能となると予測される。
計算結果のデータを下記する。最適な級数展開の次数が存在する。これは、64bit の制約と考える。
なお、下表で"真"と記載しているのは、Taylor ( Maclaurin ) 展開の解析値である。Le 、Ch は級数展開か
ら算出値で、表の級数による Taylor 係数算出値と同じである。
・正弦関数では、Legendre 多項式、Chebyshev 多項式ともに 17 次までの算出値の精度が高い。
例えば、15 次までの多項式級数展開による係数により求めた算出値と解析の真値との差が約 -14% ある
のに対し、17 次までの多項式級数展開で求めた 15 次の算出値が解析の真値との差が -0.9 であるので、
15 次までの算出値より 17 次までの算出値が精度高い事になる。
19 次までは、19 次そのもの精度が落ちている。従い、17 次までの算出値が高い。
しかし、19 次までの計算で、17 次の計算精度が高いが、これは、あらかじめ、解析値が判っているの
で、17 次が精度が高いと判断出来たのである。Legendre と Chebyshev の比較で判断出来るのでは。
・余弦関数では、Legendre 多項式、Chebyshev 多項式ともに 16 次までの算出値の精度が高い。
16 次の理由は同上である。
4-4、Maclaurin 展開の係数算出の計算例
上記で、sin( πx ) と cos( πx ) の Maclaurin 展開の係数を多項式級数展開から得た。この方法を別の関数に
適用した。その計算例の結果を記載する。以下 π は パイ(円周率) を示す。
1)多項式への適用; 5・x5 + 4・x4+ 3・x3 + 2・x2 + x + 99.99
計算結果は、上式のそれぞれの次数の係数が算出された。Maclaurin 展開の定義の通りである。
2) タンジェント tan への適用; tan( πx/3)、tan( πx/4 )
πx/3 では、9次までの係数が妥当と判断した。Legnedre と Chebyshev からの係数が同じ故。
πx/4 では、13次までの係数が妥当と判断した。Legnedre と Chebyshev からの係数が同じ故。
3)自然対数 Log; ln( x )
計算結果は、好ましいものではなかった。ln( x ) の x 軸をずらすべきである。次回の試みとする。
4)指数関数への適用; sin( 3πx )・exp( - x/2 )
Maclaurin 展開の係数は、15次までは妥当のようだ。
5)指数関数への適用; cos( 3πx )・exp( - x/2 )
Maclaurin 展開の係数は、12-13 次までは妥当のようだ。
6) 多項式との組み合わせ; 1) + 2)
問題なく、係数を得られた。
7) sin( aπx )/( aπx ) への適用; a=1.0, a=1.5, a=3, a=4.5 で計算を行った。
a=1.0 から a の値を大きくし、再構成と原関数との比較を行った。しかし、 a=4.5 以上は、原関数との
差が大きくなったので、中止した。
a=4.5, 3.0, 1.5 の時の Legendre 多項式による級数展開の再構成の図を示す。
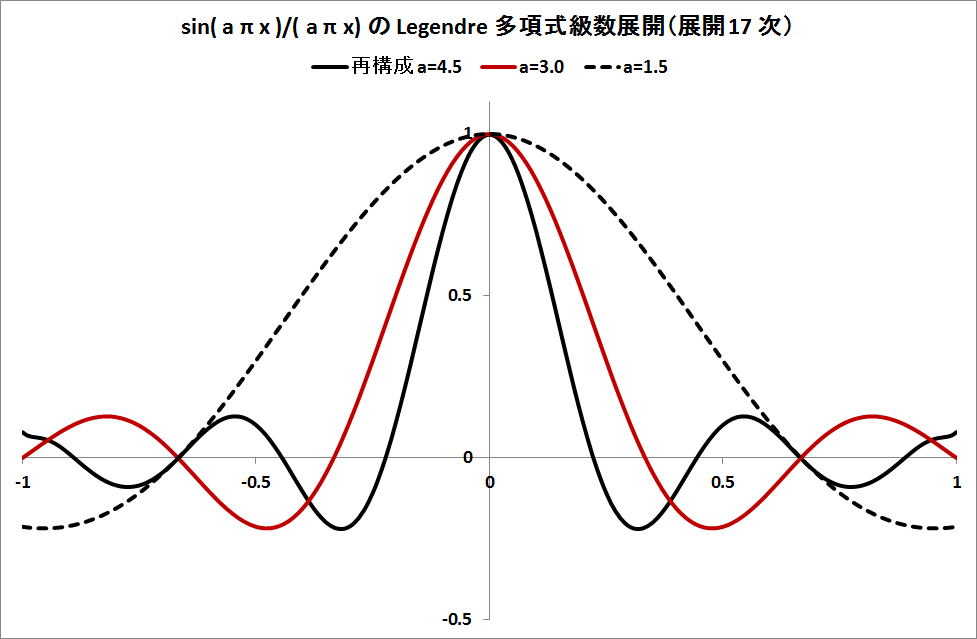
また、上図の Maclaurin 展開の係数は、提示したコードで、
a=1.5 では、16 次まで、 a=3.0 では、12 次、a=4.5 では、6 次までは近似されていると思われる。
Maclaurin 展開の係数は微分する事で得られる係数である。これを積分で算出した事になる。面白い。
Information
2012年
この章の全体履歴
2012年1月 本章を作成
2013年
この章の変更追加履歴
14)一般的な関数でTaylor展開の係数算出 2013/11/29
13)Taylor展開の係数算出 追記 2013/11/28
12)Chebyshev関数による級数展開 追記 2013/11/3
11)Legendre関数による一次結合の図の追記 2013/10/25
10)弓を引くヘラクレス に画像の差替え 2013/9/27
9)画像の追加 2013/5/3,5/6
8)Bessel 関数の追加 2013/3/28
7)画像の追加 2012/10/15
6)画像の追加 2012/9/23
5)多項式による級数展開で文意の明確化のため語句の追記2012/6/2
4)Legandre多項式による級数展開のJ1/2の記載 2012/3/16
3)Legandre多項式による級数展開の記載 2012/3/14
2)Chebyshev多項式(35次) 直交性の記載 2012/3/9
1)Legendre多項式(34)次 直交性の記載 2012/3/3


 Dhaka市内 人力車
Dhaka市内 人力車 Dhaka市内の湖
Dhaka市内の湖 Dhaka いち 12%ビール 7up 割り
Dhaka いち 12%ビール 7up 割り Dhaka 日本食堂 いち
Dhaka 日本食堂 いち
























 枕木だけの汽車道を歩いた日は何処
枕木だけの汽車道を歩いた日は何処 バッキンガム ビクトリア女王記念碑
バッキンガム ビクトリア女王記念碑 Bangladesh Dhaka 花
Bangladesh Dhaka 花  弓を引くヘラクレス アントワーヌ作
弓を引くヘラクレス アントワーヌ作  Bangladesh Dhaka 青い服の女性
Bangladesh Dhaka 青い服の女性 Bangladesh Dhaka 晴れた日の湖
Bangladesh Dhaka 晴れた日の湖 Bangladesh Dhaka 木に咲く黄色の花
Bangladesh Dhaka 木に咲く黄色の花 Jordan 渓谷
Jordan 渓谷 Jordan側より 塩湖
Jordan側より 塩湖 横浜市 港南中央近辺の道の花
横浜市 港南中央近辺の道の花 横浜市 上大岡 複合映画館入り口
横浜市 上大岡 複合映画館入り口 上大岡 京急電車
上大岡 京急電車 上大岡 京急電車
上大岡 京急電車 上大岡 銀杏と秋の空
上大岡 銀杏と秋の空 秋 柿
秋 柿 花器
花器 花
花 横浜 桜木町 ランドマークタワー
横浜 桜木町 ランドマークタワー 横浜 みなとみらい 観覧車
横浜 みなとみらい 観覧車 横浜 みなとみらい 動く歩道より北側
横浜 みなとみらい 動く歩道より北側 横浜 みなとみらい パンパシと観覧車
横浜 みなとみらい パンパシと観覧車 横浜 みなとみらい 日本丸
横浜 みなとみらい 日本丸 横浜 ランドマーク内 ハロウィンの花
横浜 ランドマーク内 ハロウィンの花 横浜 ランドマークタワー内 二階
横浜 ランドマークタワー内 二階 横浜 ランドマーク Hardrock Cafe
横浜 ランドマーク Hardrock Cafe 横浜 Queen's Square内案内
横浜 Queen's Square内案内 横浜 みなとみらい 観覧車
横浜 みなとみらい 観覧車 Bangladesh ベハラマ 赤い花
Bangladesh ベハラマ 赤い花 夕暮れの山中湖
夕暮れの山中湖 百合の花
百合の花 百合とデンフォレ
百合とデンフォレ 壁掛け London市街
壁掛け London市街 布絵 秋の外苑銀杏並木 よしかわのりこ作
布絵 秋の外苑銀杏並木 よしかわのりこ作 Dhaka 並木の中の力車
Dhaka 並木の中の力車 横浜 上大岡 並木道 往来の人(4月)
横浜 上大岡 並木道 往来の人(4月) 横浜 ランドマークタワーと日本丸(4月)
横浜 ランドマークタワーと日本丸(4月) 横浜 汽車道(4月)
横浜 汽車道(4月) 横浜 赤レンガ倉庫
横浜 赤レンガ倉庫 むくどり (赤レンガ倉庫への公園にて)
むくどり (赤レンガ倉庫への公園にて) 赤レンガ倉庫の標識
赤レンガ倉庫の標識 ドイツフェスタ in 赤レンガ倉庫
ドイツフェスタ in 赤レンガ倉庫 オランダ キューケンホフ
オランダ キューケンホフ キューケンホフ公園の花
キューケンホフ公園の花 キューケンホフ公園の花
キューケンホフ公園の花 キューケンホフ公園の花
キューケンホフ公園の花 運河
運河 チューリップ球根畑
チューリップ球根畑 キューケンホフ公園の花
キューケンホフ公園の花 キューケンホフ公園の風車
キューケンホフ公園の風車 キューケンホフ チューリップ
キューケンホフ チューリップ キューケンホフ チューリップ畑
キューケンホフ チューリップ畑 キューケンホフ 池 白鳥
キューケンホフ 池 白鳥 キューケンホフ とっとり 花回廊
キューケンホフ とっとり 花回廊 キューケンホフ とっとり 花回廊 桜
キューケンホフ とっとり 花回廊 桜 キューケンホフ 花
キューケンホフ 花 横浜/港南の路上で見たランボルギーニ
横浜/港南の路上で見たランボルギーニ キューケンホフ 運河 と かも
キューケンホフ 運河 と かも オランダ 花集荷 配送場(1)
オランダ 花集荷 配送場(1) オランダ 花集荷 配送場(2)
オランダ 花集荷 配送場(2) オランダ 花集荷 配送場(3)
オランダ 花集荷 配送場(3) オランダ 花のせり場 (築地の花版)
オランダ 花のせり場 (築地の花版) 横浜/港南 葉桜(ハッチ幼稚園の近く)
横浜/港南 葉桜(ハッチ幼稚園の近く) 横浜/港南の路上で見たランボルギーニ
横浜/港南の路上で見たランボルギーニ キューケンホフ 花々と木々
キューケンホフ 花々と木々 キューケンホフ スナックと人々
キューケンホフ スナックと人々 キューケンホフ 花と人々
キューケンホフ 花と人々 キューケンホフ 花
キューケンホフ 花