風と翼 Windandwing は、c++の数値計算から風と翼の計算へ を目的とした数値計算を行っています。

Addres http://www5.synapse.ne.jp/windandwing/
c++ 数値計算 4 Feedback回路、Euler変換、二項係数

第6章 Feedback回路、Euler変換、二項係数

概要
１、Feedback回路
高速逆ラプラス変換(FILT)を適用する主な領域は制御と微分方程式の解算出と考えられる。制御では、Feedback system の逆ラプラス変換が必要とされる。s で記述されたシステム全体を、逆ラプラス変換FILT法で、
c++のSTL/vectorの特長を活かし、算出した。結果は良好である。

2、Euler変換
高速逆ラプラス変換(FILT)では、Euler変換を適用し、交代級数の収束を速めている。このEuler変換を62次まで、算出した。この算出結果を、順次に記載していく。全面改訂前のPageでは、紙面の横幅が狭く、折り返し部分が多く、非常に見にくい状態で、公開していたが、今回は、Footer部にコードを記載するので、すこしは見やすくなると考えている。また、前章の第5章に記載するのが、betterと思われるが、5章全体が非常に長くなるので、Feedback回路の章に記載する事とした。62次まで記載しようとすると、時間がかかるので、順次に記載する。現在57次まで

3、二項係数
Euler変換は、交代級数の項を無くすと、二項係数の集合となる。従い、二項係数だけを取り出し記載した。

Feedback回路

1、Feedbackシステムの逆ラプラス変換
　　　Feedback systemで、逆ラプラス変換を求めようとすると、前処理に数ステップを踏み、実際の計算を行う
　　事になる。この事情を以下に説明する。

　　　　　　　　　　　　　　

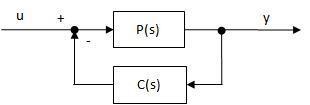
　　　　　　　　　　　　　　　　　　　　　図 1、Feedback 接続

　　　ラプラス変換の記号 s で記述されたシステム P(s) と C(s) があり、C(s) が帰還回路側に設置されている
　　図 1の Feedback 接続では、伝達関数 y/u は、式 1 のように示される。

　　　y/u = P(s) / ( 1 + P(s)・C(s) )　　　　　　　　　　　　　　　　　　　　　　　　　　 　式 1

　　　式 1 は、分母に 1 を含んだ単純な式のように見えるが、システム P(s) と C(s) 自体が単純でないので、実際
　　のシステム全体のラプラスの記号 s で示される式は、さらに複雑になる。

　　　例えば、

　　　P(s) = ( s^2 + 0.5s + 17 ) / ( s^2 + 5s + 4)、
　　　C(s) = (s^2 + 7s + 12 ) / ( s + 3 )　　　　　　　　|| 誤記訂正　s+4 を s+3 に訂正

　　　の時、

　　　y/u=(s^2+0.5s+17)/(s^2+5s+4)/(1+(s^2+0.5s+17)/(s^2+5s+4)*(s^2+7s+12)/(s+3))　式 2
　　　　　　　　　　　　　　　　　　　　　　　　　　　　|| 誤記訂正　s+4 を s+3 に訂正

　　　式 2 を、何回かの計算の後、式 3 のようにやっと整理できる。この式 3 の分母の解を算出し、部分分数に分
　　解して、教本に則し、部分分数の形により、逆変換行う。この計算もまた時間を要する。

　　　y/u = ( s^2 + 0.5s + 17 ) / ( s^3 + 5.5s + 24s + 72 ) 　　　　　　　　　　　　　　　　式 3

　　　また、下図の図 2 に示す直結 Feedback 接続の伝達関数 y/u は、式 4 で示される。

　　　　　　　　　　 　

　　　　　　　　　　　　　　　　　　　　　図 2、直結 Feedback 接続

　　　y/u = P(s) C(s) / ( 1 + P(s)C(s) )　　　　　　　　　　　　　　　　　　　　　　　　 　 　 式 4

　　この式 4 も、実際は複雑になる。

　　　従い、システムの伝達関数求める際、前処理の計算を省き、P(s) と C(s) をそのままの形で逆ラプラス変換に
　　FILTで計算する事が必要となる。

2、合成積に対するFIｌT（高速逆ラプラス変換）計算
　1)合成積の計算
　　　Feedback システムの数値計算には、式 1 に示すように合成積の計算が含まれている。合成積の計算につい
　　ては、一般に以下が成り立つ。

　　　、 の時、 の逆変換は、

　　　、

　　　、

　　　 、

　　　で計算する。


　　また、FILT計算は、以下の式に基づいている。(このHomepagenの数値計算3を参照方）

　　　　　　　　　　　　　　　　　　　式 5

　　上記のFILTの式で、合成積の計算を行う場合は、ある ｎ の時、以下の計算を行えばよい事になる。

　　　　 　　　　　 　式 6

　　式 6 は、P(s) と C(s) を同じｎで算出し、複素数値である P(sn) と C(sn) の積をとり、結果の虚数部を求
　　めると、逆ラプラス変換値を得る事ができる事になる。

　　この考えは、P(sn)=a+jb、C(sn)=c+jd　とした時、

　　　imageF(s) = image { ( a + jb ) ( c + jd ) } = ad + bc 　　 　　　　　　　　　　　　　 　式 7

　　の計算を行えばよい事になる。2 項の計算の場合は、計算精度は問題ない。

　　 これを、三項の積、P(sn)=a+jb、C(sn)=c+jd、G(sn)=e+jf に適用した場合、

　　 　imageF(s) =image { (a + jb ) ( c + jd ) ( e + jf ) } = acf + ade + bce - bdf

　　となる。しかしながら、この三項の積の場合は、計算精度に問題が生じた。四項の積の場合は、もっと複雑にな
　　り、計算精度の低下が予想される。この要因に、P(sn)等を実数部と虚数部に分けて数回計算を行う事にあると
　　、考えて、最初から、システム全体の虚数部の前処理計算が不要に出来れば、精度が良くなると考えられる。

　2)FILTでの合成積の計算と結果 (コード 1 )
　　　予め、P(sn)、C(sn) 等のための積の枠を作り、それに sn の ｍ 乗と係数 a[m] を代入して、最後に虚数
　　部を取り出す方法で計算を行った。

　　 　これで前記の式 2 の Feedback 回路について計算した結果を下図に示す。微妙な増減を計算しているので、
　　OKと言える。求値の y 値は、左側、解析解は右側で、両軸の差は 0.2 とし、両曲線が図示出来るようにした。

　　y/u=(s^2+0.5s+17)/(s^2+5s+4)/(1+(s^2+0.5s+17)/(s^2+5s+4)*(s^2+7s+12)/(s+3))　　式2
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　|| 誤記訂正　s+4 を s+3 に訂正

　　　この式 2 の逆ラプラス変換の解析解( インパルス)は、以下である。

　　　31/28exp(-4t)-3/28exp(-3/4t)cos(3/4sqrt(31)t)-73sqrt(31)/2604exp(-3/4t)sin(3/4sqrt(31)t)

　　　また、式 2 は、解析解のｙ軸の増減を、この考えで作った逆ラプラス変換コードが計算出来るかどうかを確
　　認するために作成した式である。

　　　　　　


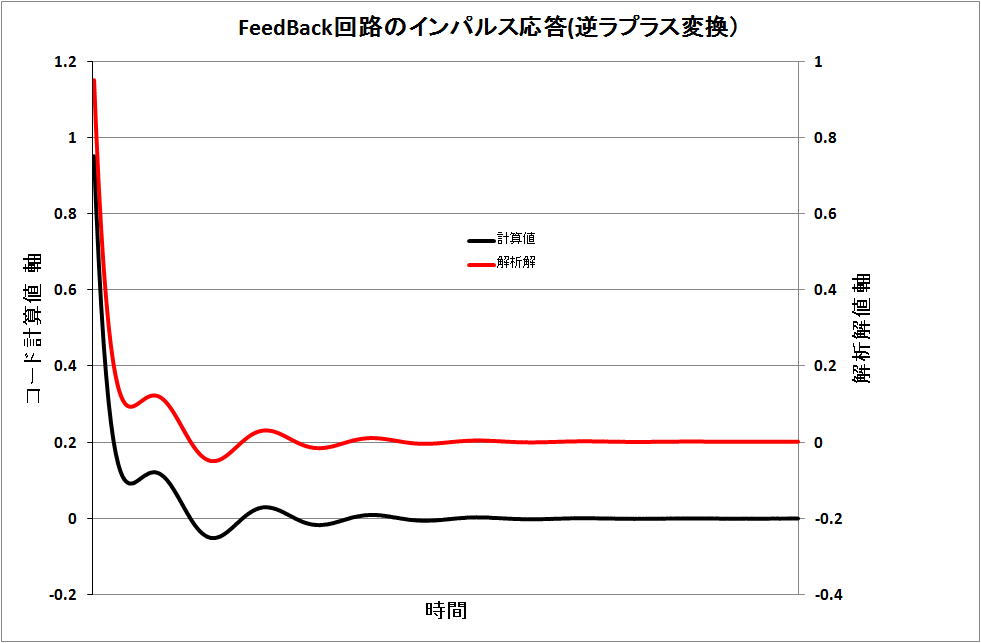
　　　更に、コードには、ステップ入力の場合の入力と解析解も記載している。この計算値と解析値を下図に
　　示す。ステップ応答でも本コードの計算は増減をよく示している。両者の差は、10-4 以下である。なお、
　　両曲線が判るように、両縦軸に 0.05 の差を設けた。
　　下図は、当然なる図であるので、Step入力にNoiseを加えた計算も下記に示す。

　　　　　　


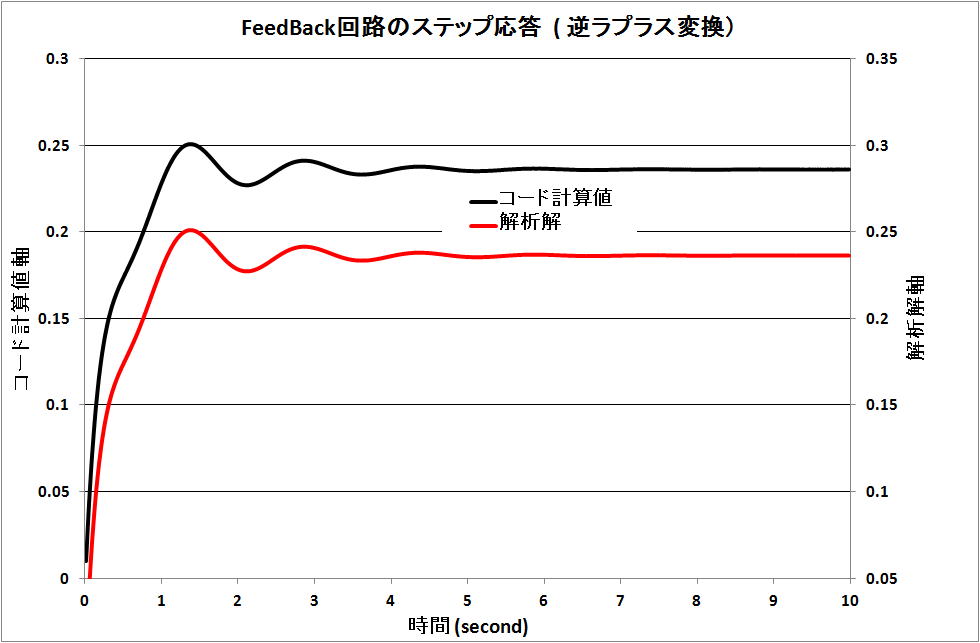
　3) 合成積に Noise を加えた場合の計算と結果
　　　上記の Step 入力に、振幅の小さな正弦波を加えた場合の計算を、周波数を変えて行う。いわゆる Noise
　　が加わった時である。
　　　小さな振幅故に、上図の直線部には小さなさざ波が生じている図になると予想できる。

　　　また、一般に、系の挙動を示す数式に、各項の係数が対象の周波数の係数と同程度であっても、それよ
　　り低周波の項や非常に周波数の高い項が生じた場合、それらの項を、系の挙動に影響を及ぼさないとして、
　　数式から除外する時がある。そのような考えを示す計算結果でもある。

　　計算は、 Step 入力( 1.0 )に 0.025・sin(a・t) を加える。ただし、 a= 0.2 , 2 , 20 , 200 (rad/s) とする。

　　即ち、1/s + 0.025・0.2/(s2+0.22) , 1/s + 0.025・2/(s2+22) , 1/s + 0.025・20/(s2+202) ,,,
　　
　　具体的には、

　　　1/s + 0.025・0.2/(s2+0.22) = (0.22 + 0.025・0.2・s + s2)/(0 + 0.22・s + s3)

　　となるので、コード 1 の Step の個所

　　　//Step 1/s　の分子入力の設定
　　　//a1[0]=1.0;// 1/sの 1 の入力
　　　//b1[0]=0.0;b1[1]=1.0;// 1/(s+0.0)の0.0とsの係数1.0の入力


　　を変更し、以下で計算する。

　　・ a ＝ 0.2 の時　sin(0.2t) を加えた時
　　　//Step+0.025*sin(0.2t) =1/s+0.025*0.2/(s^2+0.2^2)　の分子側入力の設定

　　　上記の式の分数の和は、以下の式となる。

　　　( 0.04 + 0.2*0.025*s + s^2 ) / ( 0.04*s + s^3 )

　　　従い、分母側はコード 1 のままで分子側は以下となる。

　　　a1[0]=0.04;a1[1]=0.2*0.025;a1[2]=1.0;
　　　b1[0]=00000.0;b1[1]=0.04;b1[2]=0.0;b1[3]=1.0;

　　・ a ＝ 2 の時　　sin(2t) を加えた時
　　　//Step+0.025*sin(2t) =1/s+0.025*2/(s^2+2^2)　の分子側入力の設定

　　　上記の式の分数の和は、以下の式となる。

　　　( 4.0 + 2.0*0.025*s + s^2 ) / ( 4.0*s + s^3 )

　　　従い、分母側はコード 1 のままで分子側は以下となる。

　　　a1[0]=4.0;a1[1]=2.0*0.025;a1[2]=1.0;
　　　b1[0]=00000.0;b1[1]=4.0;b1[2]=0.0;b1[3]=1.0;

　　・ a ＝ 20 の時　　sin(20t) を加えた時
　　　//Step+0.025*sin(20t) =1/s+0.05*20/(s^2+20^2)　の分子側入力の設定

　　　上記の式の分数の和は、以下の式となる。

　　　( 400.0 + 20.0*0.025*s + s^2 ) / ( 400.0*s + s^3 )

　　　従い、分母側はコード 1 のままで分子側は以下となる。

　　　a1[0]=400.0;a1[1]=20.0*0.025;a1[2]=1.0;
　　　b1[0]=00000.0;b1[1]=400.0;b1[2]=0.0;;b1[3]=1.0;

　　・ a ＝ 200 の時　sin(200t) を加えた時
　　　//Step+0.025*sin(200t) =1/s+0.025*200/(s^2+200^2)　の分子側入力の設定

　　　上記の式の分数の和は、以下の式となる。

　　　( 40000.0 + 200.0*0.025*s + s^2 ) / ( 40000.0*s + s^3 )

　　　従い、分母側はコード 1 のままで分子側は以下となる。

　　　a1[0]=40000.0;a1[1]=200.0*0.025;a1[2]=1.0;
　　　b1[0]=00000.0;b1[1]=40000.0;b1[2]=0.0;b1[3]=1.0;


　　・ a = 0.2 , 2 (radian/s) の時を下図に示す。
　　　0.2 の時は、系に sin(0.2t) の挙動は現れていない。2 の時は、sin(2t) の挙動が現れている。
　　　従い、低周波の時に、その項を考慮しないでよいと考えてもいいという結果である。

　　　　　　


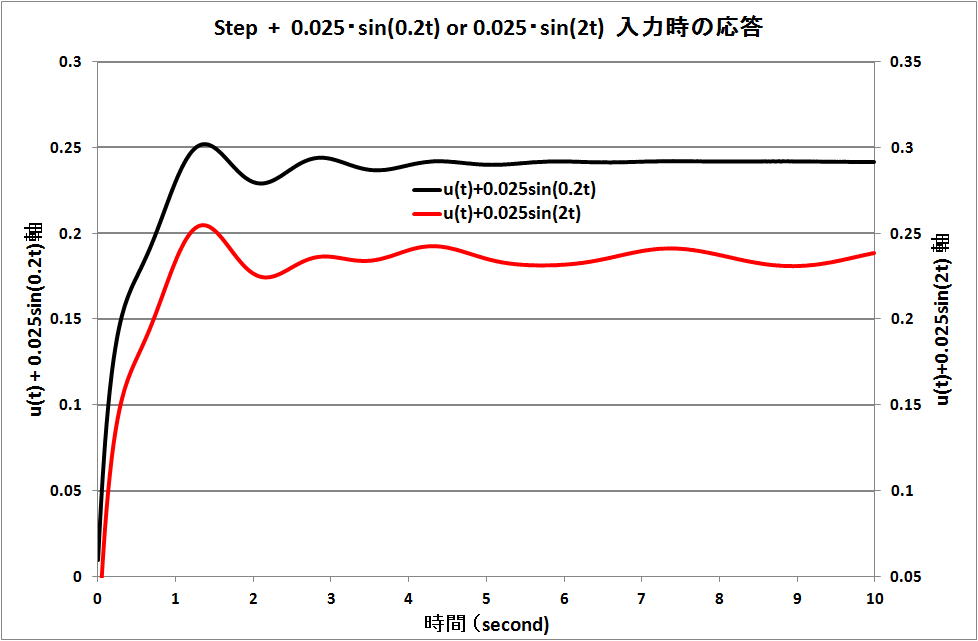
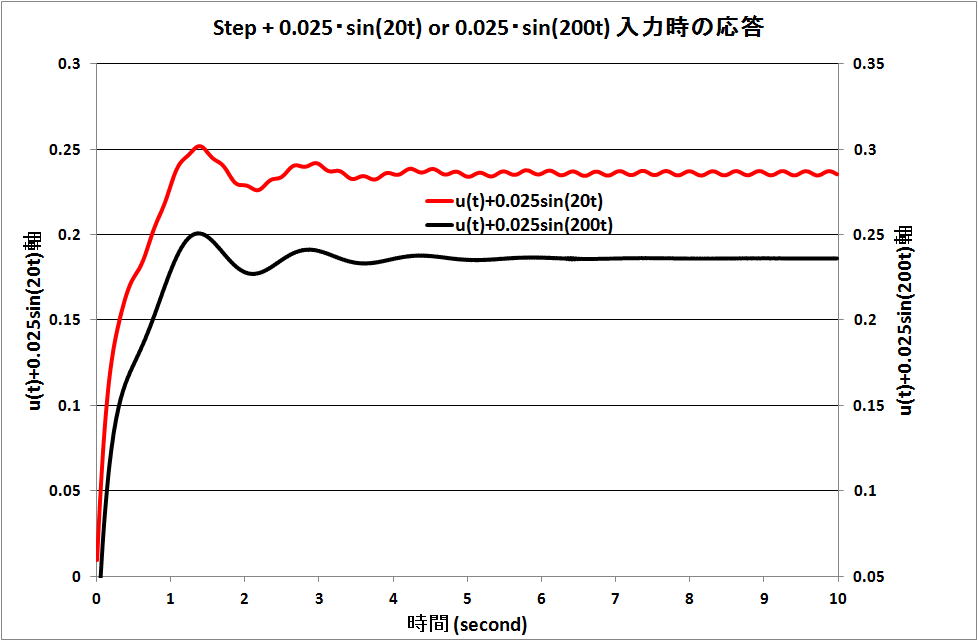
　　・ a = 20 , 200 (radian/s) の時を下図に示す。
　　　20 の時は、系に sin(20t) の挙動が現れている。200 の時は、sin(200t) の挙動が現れていない。
　　　従い、高い高周波の時には、その項を考慮しないでよいと考えてもいいという結果である。

　　　　　　



　4)Feedback回路の具体的な計算(コード1)
　　(1)コードの説明
　　　　・予めP(s)等の数を 8 とした。それらの積で計算するようにした。

　　　　・その係数を分子、分母伴に 最大 7 次とした。細野本等では5次であったので、+2とした。

　　　　・その係数を TR1 の array に代入するようにした。
　　　　　しかしながら、array　のfunction文内の宣言では、コンパイラーから、その記述の以外にも、配列の個
　　　　　数を求められた。煩雑感を与える式となった。vectorでは、vector<double>の表示だけでよかったが。

　　　　 ・係数 a0[0] 等の初期値を 1.0 にすることで、0 の積を無くし、システムがゼロにならないようにした。

　　　　 ・Feedbackシステム全体では、(1+P(s)・・・) が分母になるので、1 を含めないで、積の個所だけを計
　　　　　 算し、その後に real_unit で複素数化した 1 を付け加えるようにした。

　 　　　・Feedbackシステム (1+P(s)・・・) 適用の有無を feedwith で選択できるようにした。

　　　　 ・計算自体の失速防止のために、単純和の項数 k 制御の function 文を設けた。第5章逆ラプラス変換 3項
　　　　　 (項数 k の制御計算を判りやすくした。)

　　　　 ・Euler変換は 61 次で固定した。これは発散・失速が初期の数項の実数部と虚数部の位相が同じ位相面に
　　　　　 留まっている（複素平面上で同位相面にある）時に生じるので、変換の次数と直接な関係は無い事が判
　　　　　 っているために、61 次に固定とした。C++11 で long double が 64bit 以上になれば、もっと次数を
　　　　　 高く出来るのだが、今は叶わない。

　　　　・高速ラプラス変換の細野本で定義されていた打ち切り誤差の評価は、ここでは削除した。


　 (2)ボード線図用データ
　　　第5章で、Bodeplot について、説明しているが、ここでもコード内で計算できるようにしたので触れる。
　　　上記の式 5 の s = ( a + j( n - 0.5 ) π ）/ｔ (π:パイ) の複素数 s の実数部の a 、ここでは filt_a=0.0 およ
　　　び、0.5 を 0 、(パラメータ spare0=0 )にすることで、得る事が出来るようにした。

　　　具体的な、コードの記述を下記にしめす。下記の作業を行うと本コードでも計算できて、出力される。

　　　　//Bode_Plot 用 以下の5行のそれぞれの初めにある　//　を削除するとBode Plot 用に変化する。
　　　　//filt_a=0.0; //s の実数部をゼロにし、s の虚数部のみとする。
　　　　//k1=100;     //nick=31.4の時、k1 は、f を 0.1 から 10rad/s 変化させる
　　　　//nick=31.4;  //π/31.4 は 0.1 となる。
　　　　//repeat_no=2;//繰返し数が 2 未満であるので、1 回計算する。
　　　　//spare0=0;   //0 の時、s の虚数中の -0.5 がゼロ。

　　　次は、ゲインによるシステムの安定性の計算をFILTで容易に出来るようにする考えである。

3、使用したSTLと関数
　1)array<double,n>、vector<complex<double>>、ofstream()、fraction[2].real(real(data))。

　2)TR1::arrayについて
　　array<complex<double>,n>x は、許容される。しかしながら、虚数部の数値は得る事ができなかった。
　　再度、行う予定であるが、arrayでの複素数使用の際は、注意が必要である。

　　　

Euler変換

1、Euler変換の説明
　 　ここでは、逆ラプラスを行うための準備として、62 次までのEuler変換の計算式を示した。書籍では、一般に
　6 次程度までの Euler 変換により収束させる事が行われているが、10 倍の 62 次になれば、どの程度までの収束
　になるのか知るためである。現在 57 次まで記載。

　　Euler 変換は、無限級数　1-1/3+1/5-1/7+・・・のような交代級数（ 1 式）に

　　　　　　　　　　　　　　　　　　 　　 　　　　　式 1

　 　下記のような操作を施して、和を求める計算方法で Euler が考え出した。

　　　
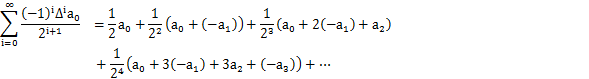
　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 式 2


　　式 1 のマイナス項をかっこ内に入れた時、各項の定数係数の関係は、式 2 のように二項係数になっている。
　　Euler変換の説明は、インターネットでは、南中野パソコン教室(tolyo-pax.co.jp)や長田直樹氏や大浦拓哉
　　氏のHomePage、書籍では"計算数学夜話"や"C言語の科学技術計算"にある。これらでは、差分演算子Δを使用し
　　、簡潔な方法で示されている。簡潔に表現されているために、ΔやDの記号の意味を取り違えやすい。

　　なお、二項係数(n,r)は n!/(n-r)!/r! を示す。ここで、重要となる二項係数（ｎCｒや（ｎ,ｒ））の算出について
　　は、下記の二項係数の節に示す。

2、Euler変換(コード2) 　現在、57次まで記載
　1)Euler変換の算出 式 2 の計算には2つの方法が考えられる。

　　・第一番目の方法
　　　それぞれの項のｎ次毎に、二項係数と要素 a[r]との積の和、即ち、(ΣnCr・a[r])/2^(n+1)を逐次算出し、更
　　　に、それぞれの(ΣnCr・a[r])/2^(n+1)項の n 次までの和を式 2 のように求めた計算。
　 　　例えば、

　　　 　0 order：a0/2
　　　 　first 　 ：(a0 + (-a1))/22
　　　 　2nd　　：(a0 + 2(-a1)+a2)/23
　　　 　3rd 　　 : (a0 + 3(-a1)+3a2+(-a3))/24

　　　とした時、

　　　 　0次のEuler変換：0 = a0/2
　　　　 1次のEuler変換 : 0 + 1st = a0/2 + (a0 + (-a1))/22
　　　　 2次のEuler変換 : 0 + 1st + 2nd = a0/2 + (a0 + (-a1))/22 + (a0 + 2(-a1)+a2)/23
　　　　 3次のEuler変換 : a0/2 + (a0 + (-a1))/22 + (a0 + 2(-a1)+a2)/23+(a0 + 3(-a1)+3a2+(-a3))/24

　　　のように、Euler 変換を行っていく方法。

　　・第二番目の方法
　　　式 2 の
　　　　　　 a0 だけに注目すれば、 a0・( 1/2 + 1/2^2 + 1/2^3+ …）、
　　　　　 　 a1 だけに注目すれば、 a1・( 1/2＾2 + 2/2^3 + 3/2^4+…）、
　　　 　 　　a2 だけに注目すれば、 a2・( 1/2＾3 + 2/2^4 + 3/2^5+…）、

　　　が成立するので、ｎ次まで毎に、a0、a1、a2、・・・ an を一括して合計した計算。
　　　これには、各項の係数の大小順が生じるので、係数の大小で、二通りがある。

　　これら三つの方法により、下記のように、Euler 変換による収束計算を行った。

　2)Euler変換による数値計算のコードの説明(コード2)
　　・コンパイラー　MS社のVS2008.
　　・定数係数の確認
　　　二項係数を 62 次まで算出した。15桁の制約があり、一部、手計算で 2 のpower計算等を行った。また、
　　　Euler変換の各項を 1 として計算を行い、2 の n 乗との比較を行い、定数係数に誤りが無い事を確認した。

　　・三つの方法で計算
　　　第一番目に対応した、各次数での和 (euler::delta) を逐次求めるものをEuler::step1、
　　　第二番目の一括して計算する方法で項の係数の数値の大から順次、和を求める方法をEuler::step2、
　　　第二番目の係数が小さい方からの和をEuler::step3とした。
　
　　・打ち切り誤差をeuler::trancationで算出した。これは細野本の定義に準じた。

　　・なお、定数係数だけを抜き出した配列をコードの後半部に示す。
　　

　3)数値計算結果
　　・結論
　　　計算精度の高い順：Euler::step3が一番高く、step2、step1で低下する。 64bit の制約がstep1では早い。

　　・交代級数の対象計算例
　　　π/4、log2.0、π・π・π/32、高速ラプラス変換の参考例 π/4・sech(π/2))　(π：パイ)
　　　　　　上記 log2.0 以下の後ろの3つは、コードでは、/*...*/ で控えた。

　　・対象の計算結果
　　　計算結果は想定通りであった。次数が高くなると収束の度合いは高くなる。
　　　また、打ち切り誤差euler::trancation値は58次等の高い次数では、doubleの精度限界の丸め誤差の影響によ
　　　り、真値とeuler変換値との差より、小さいなった。本来ならば、打切り誤差は、大きくなければならない。

　　・パイ (π) の計算結果
　　　Euler 変換によるパイ (π)/4 の収束の計算結果を Euler 変換の次数毎に示す。4*step3 の条件の時が早い。
　　　Euler 変換の次数から言えば、step3 の手法で、50 次以上であれば 10 の -16乗を確保できる事になる。
　


3、使用したSTLおよび関数
　　reverse_copy、accumulate

4、感想
　　Euler は、Euler の公式、 Euler 変換のみならず、多くの π (パイ) の算出計算を行っている。
　　 参考　オイラーの無限解析　2001年　海鳴社　高瀬正仁氏訳
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 　　　　　　　　　　　　　　　　　　　

二項係数

1、二項係数算出(再帰計算、逐次計算法)(コード3)　現在、57次まで記載
　　 Euler 変換では、二項係数を定数係数として利用しているので、これを再帰法と逐次法で算出した。

　1)再帰法
　　この nCr、即ち Combination(n,r) では、function 文での条件が重要である。書き忘れると疑問な数値
　　が生じる。再帰には、　nCr=n-1Cr+n-1Cr-1 を利用した。

　　また、29 次以上では再帰法は、計算に時間を要する。このため、30 次以上は逐次法が良い。

　　コードで再帰の個所の抜書きを下記に示す。

　　　long long Combination(int n, int r)//n!/((n-r)!*r!)
　　　　{
　　　　　if(n == r || !r) return 1;//Combination(n,n)=1
　　　　　if ( r == 1 ) return n; //Combination (n,1)=n
　　　　　if(n < 0 || r < 0 || n < r) return 0;//条件文が必要。
　　　　　return Combination(n-1,r) + Combination(n-1,r-1);
　　　　}

　2)逐次計算法
　　30 次を再帰法で計算し、この 30 次のそれぞれ要素と一つずらした要素を合算し、31 次を得た。
　　二項係数は一つ前のデータから順次高い次数を得る事が出来る。これは、二項係数の算出が、例えば、
　　(1+a)^(n+1) が (1+a)^n に (1+a) を掛ける事であるためである。

　　即ち、

　　　[(1+a)^nの数列]×(1+a) ＝ [(1+a)^nの数列]×1 ＋ [(1+a)^nの数列]×a

　　となり、a の次数の高い隣の要素と合算すれば、ｎ+1 次の二項係数を逐次に得る事が出来る事になる。
　　(隣との和は、accumulateを利用すれば簡単になるが今回は採用しなかった。)

　　なお、49 次以上の各係数の出力は、 txt ファイルが良い。数値の丸め（1桁等の 0 表示）が減る。
　　このために、49次以上は、前述したように、手計算で、算出した。

2、使用したSTLおよび関数
　　push_back、resize(x.size())


　　　　　
2012年1月
この章の履歴
2012年1月9日　再公開　
2012年
この章の変更追加履歴
 12、Stepに高低周波数のノイズの入力説明 2014/2/3
11、Euler変換による計算結果の例の記載 2012/12/30
10、写真の追加 2012/9/17
9、写真の追加 2012/9/15
8、Feedback回路の y/u 2式の4→3 の誤記訂正　2012/8/25
7、Euler変換・二項係数を57次まで　2012/7/3
6、Feedback回路の節で、Step入力に低周波・高周波を
　 　加えた時の応答を追加、誤記を変更 2012/7/1
5、Feedback回路の節でStep応答の図を追加 2012/6/19
4、Euler変換・二項係数を55次まで、　2012/5/27
3、Euler変換・二項係数を52次まで、　2012/2/22
2、Euler変換・二項係数を47次まで、二項係数の再帰を抜書き2012/1/29
1、Euler変換に、説明文を追記　2012/1/10
　
　　

ナビゲーション


　フランクフルト Goethe hous

　フランクフルト Goethe hous

　花 花 花

　横浜 ベイブリッジ

　フランクフルト ゲーテ像

　川崎 大師幼稚園 園長胸像

　横浜 ランドマーク 彫像

　横浜 ランドマーク 通路

　花

　芦ノ湖 海賊船

　芦ノ湖 遊覧船

　横浜 みなとみらい

　鎌倉 八幡宮様の石の階段 銀杏の木

　Liberia モンロビア近郊の河川

　Liberia 街道沿いの商店街

　Liberia Casa Hotel Entrance

　横浜駅 西口側付近の空

　横浜駅 東口側より

　Ghana Accra Novotel Hotelの木々

　ロープウェイ 大涌谷へ

　横浜 港南区 夜景

　箱根マイセンアンティーク美術館

　花

　空蝉と青い柿の実

　ガラスと枝

　ほのかな光の回廊

　ほのかな光のビーズ展

　煌くヴェネチアンビーズ展

　花々 箱根ガラスの森美術館

　箱根ガラスの森美術館

　花と花 箱根ガラスの森美術館

　枯れ木のオブジェと喫煙する人

　小田原 箱根登山電車

　芝生に立つ枯れた木のオブジェ

　翼の間より見る冬の日本海

磯子プリンスホテル 植物園 花